这个月月初就开始看《从一到无穷大》，花了接近两个星期才看完。这确实是一本让人放不下手的好书。考虑到我的阅读速度，一个多星期一本书已经近乎神速了。在这本书里我经常会看到一些有趣的数学知识，前段时间我还写过书里提到的一个有趣的东西——环面上的染色问题反而比平面上的“四色问题”更加简单。这种例子并不罕见，很多时候一些扩展版的问题反而比原问题更加简单。在第八章，我看到了另一个好玩的东西：随机游走(random walk)问题。
    随机游走问题是说，假如你每次随机选择一个方向迈出一个单位的长度，那么n次行动之后你离原点平均有多远（即离原点距离的期望值）。有趣的是，这个问题的二维情况反而比一维情况更加简单，关键就是一维情况下的绝对值符号无法打开来。先拿一维情况来说，多数人第一反应肯定是，平均距离应该是0，因为向左走和向右走的几率是一样的。确实，原点两边的情况是对称的，最终坐标的平均值应该是0才对；但我们这里考虑的是距离，它需要加上一个绝对值的符号，期望显然是一个比0大的数。如果我们做p次实验，那么我们要求的平均距离D就应该是

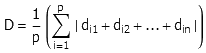
    其中d的值随机取1或者-1。这里的绝对值符号是一个打不破的坚冰，它让处于不同绝对值符号内的d值无法互相抵消。但是，当同样的问题扩展到二维时，情况有了很大的改变。我们把每一步的路径投射到X轴和Y轴上，利用勾股定理我们可以求出离原点的距离的平方R^2的值：

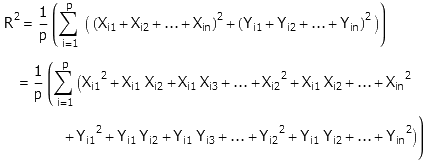
    一旦把平方展开后，有趣的事情出现了：这些X值和Y值都是有正有负均匀分布的，因此当实验次数p充分大时，除了那几个平方项以外，其它的都抵消了。最后呢，式子就变成了

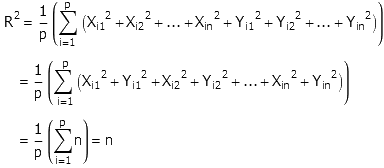
    于是呢，就有平均距离R=sqrt(n) （准确的说是均方根距离）。我们得出，在二维平面内随机选择方向走一个单位的长度，则n步之后离出发点的平均距离为根号n。这是一个很美妙的结论。

    有些时候，数学世界和物理世界会奇迹般地结合起来，碰撞出绚丽的火花。这个Blog之前就曾经写过一系列用物理方法解决数学问题的例子。在这里，这一个简单的随机游走定律同样对应了一个极其普遍的物理现象：Brown运动。你会发现，不管是水中墨滴扩散，两种液体的混合，还是热导体中的传热，都遵循一个简单的定律：扩散的距离与时间的平方根成正比。事实上，这本书花了相当大的篇幅来讲解这几种物理现象及其扩散速度定律的意义。
    “从一到无穷大”这个名字会让人误以为这本书是一本数学书。其实，这本书里面的数学知识只占了很小的一部分。这是一本贯穿各大科学领域的科普读物，书里面从数字讲到空间和维度，引出Einstein的时空观念，试图揭示宇宙的时空本质；进而乘坐“下降的阶梯”进入微观世界，从化学一直谈到生物；最后我们将再次迈入宇宙空间，进入神秘莫测的宇宙学。
    作为一个（形式上的）文科生，我很高兴能够以这种方式学习到理科的各种基础知识，而不是被应试教育强迫地灌进各种做题所需的知识和技巧；后者必然会减少很多乐趣。

    大概有三四年没有接触物理了吧，但对物理的钟爱一直未减。我经常说起一句很经典的话，这非常确切地表达出我对数理化孰轻孰重等问题的看法：Chemistry is physics without thought. Mathematics is physics without purpose. 不知道为什么，我就是非常讨厌化学，或许这种厌恶是来自于化学本身的一些非逻辑性。即使看完了《从一到无穷大》，我仍然觉得，除了元素周期以外，其它的很多东西都是不成逻辑体系的牵强附会。或许这是一种偏见，或许这只是我认识不够深，总之我因为化学成绩太差，高一下学期被迫选择了文科。但我一直舍不得物理学，开始文科学习的头半年仍然被惯性驱动着，读完了物理的高中教材。物理和数学都有其独特的魅力：数学美在其精巧的证明，物理则美在巧妙的实验设计。第一个想出用水银代替普通液体测量大气压强的人真的是天才，用镜片的细小扭动把万有引力放大到肉眼可见的尺度似乎是人类在向大自然高呼自己并不渺小。物理实验最震撼的就是，凭借一些并不复杂但却异常巧妙的装置，我们可以观测出比自己大很多很多的尺度下的物理现象。

    说起大尺度，估计没什么比得过光速了。最初试图测量光速的做法是可笑的：Galileo和它的助手站在郊外旷野，彼此相距好几英里远，然后Galileo打开遮光板并开始计时，助手在远处看到光线后立即打开他那边的遮光板，最后Galileo看到对方过来的光线并停止计时。当然，现在我们知道，光的速度太快了，一秒钟足以绕地球七圈半，而在这个时间里他助手的手脚甚至还反应不过来。说来有趣，Galileo用实验的方法得知了他的实验是没有意义的：当他和他助手之间的距离扩大一倍后，测出来的时间还是一样的，并未随距离的扩大而翻倍。于是Galileo意识到：光的速度值是可怕的，这种传统的方法根本测量不出来，所得到的时间间隔仅仅是“反应迟误”。
    法国物理学家Fizeau真是一个天才！他用一个小小的仪器精确地得到了光的速度。把两个同样规格的齿轮安装在同一根转轴的两侧，并让这两个齿轮正好齿和齿缝错开来相对。在转轴的其中一头放置一个光源，则（转轴静止时）从转轴的另一头向光源看过去，两个齿轮重叠的方式正好挡住了对面全部的光线。然后我们开始转动转轴，转轴带动两个齿轮以相同的速度转动。当转速到达一定值时，我们会观察到一个神奇的现象：两个齿轮的齿缝似乎对在了一起，那一端的光线直接从齿缝间穿过来了。这是因为光线在两个齿轮间传播的过程中，齿轮正好转过了半个齿，于是当光线到达第二个齿轮时原本齿的位置就变成了齿缝，光线就这样通过了两个本来错位相对的齿轮。如果此时再以双倍的速度转动转轴，则齿与齿之间的缝隙就又不见了，因为光线传播的时间里齿轮正好转过整整的一个齿。根据转速和齿轮的规格，我们就可以计算出光速的值。为了让实验更加精确，我们可以在光线传播的途中多加一些镜子来延长光路。

    人类所面临的第一个超越自己尺度的物体或许就是我们脚下的大地。有时候我们会觉得奇怪：古人是怎么发现地球是圆的呢？事实上，要发觉这一点并不困难，自然界中有相当多的征兆预示着“地面是弯曲的”这一事实。例如，一艘船消失在地平线时，总是船身已经看不见了，但桅杆还露在水面上。地球是一个球体，这意味着我们脚下的大地是有限的。那么，这个世界到底有多大呢？想要测量出地球的大小似乎是不可能的，因为我们本来就生活在地球上，人类似乎面临着一个“抓着头发把自己提起来”的难题。公元前3世纪，Eratosthenes想出了一个绝妙的办法：当阳光垂直射入A城的竖井时，在800公里外的B城测得日光与地面有7度的夹角。我们立即可知，地球圆周的1/50长大概是800公里，那么整个圆周长度就是40000公里左右了。
    测量地球的大小还不算牛B，人类所干的牛B事儿多了去了。比如，我们是怎么知道月球距离我们有多远的？尽管我们仍然面临着更加严重的“只缘身在此山中”难题，但科学家们还是把它解决了。为了说明这个问题，不妨让我们看一个同样是远距离地测量处于自身之外的物理量，但更具有启发性的问题：“目测”是如何工作的？这让我们想起一个很有趣的小游戏：睁一只眼闭一只眼穿针相当困难，但两只眼睛一起用的话线一下子就穿进去了。只用一只眼睛看东西会失去立体感。我穿针相当的笨，曾经一度以为那是我手脚不灵活，但后来我开始设想是不是由于我眼睛分辨不出深度的问题。我很可能从来没感受过真正的“立体感”，因为我的左眼有严重的散光和弱视，因此我看东西几乎可以说是只用到了右眼。说了半天，为什么两只眼睛看东西就能分辨远近呢？这是因为，由于角度的原因，两只眼睛看到的画面并不是完全相同。不断换用左右眼来看东西，你会发现，距离你近的东西会在远景上产生一定的位移。这就是所谓的“视差”，我们的大脑能够根据两眼所获得的视差来判断距离。同样的方法仍然可以适用于在地球上观察月球，只是为了产生更大的“视差”，我们的两只“眼睛”应该相离足够远才行。天文学家们从地球的两端同时对着月球拍照，算出视差为1°24’5”，从而得知地球和月球之间的距离为地球直径的30.14倍，即384403公里。
    当然，存在一些更远的星星，即使地球两端这么远的距离仍然不能造成足以观测到的视差。这下怎么办呢？德国天文学家Bessel突发奇想，企图利用地球在公转轨道上的不同位置所造成的视差来测量距离！1938 1838年，他开始对相隔半年的星空进行比较，发现一颗天鹅座的恒星在星空背景中有了些许的位移。然而，再过半年重新进行观测时，这颗恒星又回到了一年前的位置，这说明了半年前的位移确实是由视差造成的，而不是星星本身的移动。根据这个视差，Bessel计算出这颗恒星在103 000 000 000 000公里之外，比太阳还远690 000倍！人类似乎一下子变得异常的高大，人类文明的双手伸向了太阳系外的星球，而Bessel就是拿着尺子跨出太阳系进入星际空间的第一人！
    大家当然会问，那更远的星星呢？事实上，尽管视差法已经不再凑效了，但我们也有别的测量方法。甚至包括银河系的样子、银河系的旋转、地球的年龄、宇宙的年龄这样一些天文尺度下的物理现象和物理量，我们也能从一些细小的线索中逐步推测出来。以前一直在想，人们是怎么知道地球的公转和自转，又是如何知道地球的年龄和形成过程的；从这本书中我找到了答案，并且由衷地感叹人类思维的无穷力量！在宇宙的大尺度下，人类或许很渺小，但思维绝对不受任何尺度的限制！从一走到无穷大的，不仅是指几千年来的数学史，更是整个人类文明的思想和智慧。

 
    最后呢，和大家分享书上的一段有趣的文字。