在去年10月份的数学文化节期间，我去听了好几次讲座，其中有一些讲的相当精彩。时间过得好快，转眼间又是一年了，如果不是Wind牛发短信问我去不去听讲座，我估计今年数学文化节过了都还想不起这档子事。于是和Wind牛跑去二教309，听了一场叫做《从数据中挖掘因果关系》的讲座。这个题目是很有趣的：数据本身并不说谎，难就难在我们如何从中挖掘出正确的信息。当我们讨论数据时，我们讲的最多的是数据的相关性，而我们希望得到的则是事件之间的因果联系；但事实往往是复杂的，统计数据有相关性并不意味着两个事件具有因果联系，而具有因果联系的两件事从统计数据上看有时也并不相关。
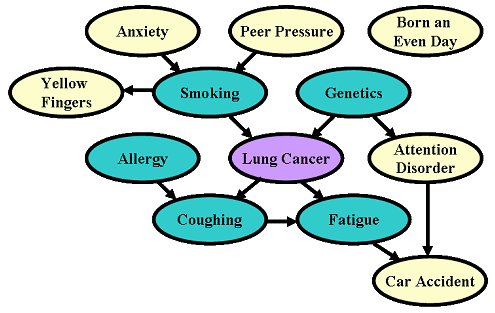
    对于前者，最简单的例子就是公鸡打鸣与太阳升起：公鸡打鸣与太阳升起总是同时发生，但这并不表示把全世界所有的公鸡都杀光了后太阳就升不起来了。统计发现，手指头越黄的人，得肺癌的比例越大。但事实上，手指的颜色和得肺癌的几率之间显然没有直接的因果联系。那么为什么统计数据会显示出相关性呢？这是因为手指黄和肺癌都是由吸烟造成的，由此造成了这两者之间产生了虚假的相关性。我们还可以质疑：根据同样的道理，我们又如何能从统计数据中得出吸烟会致癌的结论呢？要想知道吸烟与癌症之间究竟是否有因果联系的话，方法很简单：找一群人随机分成两组，规定一组抽烟一组不抽烟，过它十几年再把这一拨人找回来，数一数看是不是抽烟的那一组人患肺癌的更多一些。这个实验方法本身是无可挑剔的，但它太不道德了，因此我们只能考虑用自然观察法：选择一些本来都不吸烟的健康人进行跟踪观察，然后呢，过段时间这一拨人里总会出现一些失意了堕落了犯上烟瘾的人，于是随着时间的流逝这帮人自然而然地分成了可供统计观察的两组人。注意，这里“是否吸烟”这一变量并不是随机化得来的，它并没有经过人为的干预，而是自然区分出来的。这是一个致命的缺陷！统计结果表明，犯上烟瘾的那些人得肺癌的几率远远高于其他人。这真的能够说明吸烟致癌吗？仔细想想你会发现这当然不能！原因恰似黄手指与肺癌一例：完全有可能是某个第三方变量同时对“爱吸烟”和“患肺癌”产生影响。1957年，Fisher提出了两个备选理论：癌症引起吸烟（烟瘾是癌症早期的一个症状），或者存在某种基因能够同时引起癌症和烟瘾。
    有虚假的相关性数据，就有虚假的独立性数据。“健康工人效应”是一个特别有意思的理论。调查发现，在铀矿工作的工人居然与其它人的寿命一样长（有时甚至更长）。这表明在铀矿工作对身体无害么？当然不是！其实，是因为去铀矿工作的工人都是经过精心挑选的身强体壮的人，他们的寿命本来就该长一些，正是因为去了铀矿工作才把他们的寿命拉低到了平均水平。这一有趣的细节导致了数据的伪独立性。类似地，有数据表明打太极拳的人和不打太极拳的人平均寿命相同。事实上呢，太极拳确实可以强身健体、延长寿命，但打太极拳的人往往是体弱多病的人，这一事实也给统计数据带来了虚假的独立性。

    现实中的统计数据往往会表现出一些更加诡异复杂的反常现象。Simpson悖论是统计学中最有名的悖论：各个局部表现都很好，合起来一看反而更差。统计学在药物实验中的应用相当广泛，每次推出一种新药，我们都需要非常谨慎地进行临床测试。但有时候，药物实验的结果会让人匪夷所思。假设现在我们有一种可以代替安慰剂的新药。统计数据表明，这种新药的效果并不比安慰剂好：

         有效   无效   总人数
新药      80    120     200
安慰剂   100    100     200

    简单算算就能看出，新药只对40%的人有效，而安慰剂则对50%的人有效。新药按理说应该更好啊，那问题出在哪里呢？是否是因为这种新药对某一类人有副作用？于是研究人员把性别因素考虑进来，将男女分开来统计：

       男性有效  男性无效  女性有效  女性无效
新药      35        15        45       105
安慰剂    90        60        10        40

    大家不妨实际计算一下：对于男性来说，新药对高达70%的人都有效，而安慰剂则只对60%的人有效；对于女性来说，新药对30%的人都有效，而安慰剂则只对20%的人有效。滑稽的一幕出现了：我们惊奇地发现，新药对男性更加有效，对女性也更加有效，但对整个人类则无效！

    这种怪异的事屡见不鲜。前几个月一个高中的师弟给我发短信，给了我两个大学的名字，问该填报哪个好。鉴于我目前的悲惨境遇，我非常认真地帮他查了一下两所大学的男女比例，并且很细致地将表格精确到了各个院系。然后呢，怪事出现了：A学校的每个院系的女生比例都比B学校的同院系要高，但合起来一看就比B学校的低。当然，进错了大学找不到MM是小事，大不了像我一样20岁了连初吻都还没有，拿出去丢丢人让别人笑话笑话就完事了；但医药研究需要的是极其精细的统计实验，稍微出点差错的话害死的可就不是一两个人了。上面的例子再次告诉我们，统计实验的“随机干预”有多么重要。从上面的数据里我们直接看到，这个实验的操作本身就有问题：新药几乎全是女的在用，男的则大都在用安慰剂。被试者的分组根本没有实现完全的随机化，这才导致了如此混乱的统计结果；不难设想，如果每种药物的使用者都是男女各占一半，上述的悖论也就不会产生了。当然，研究人员也不都是傻子，这么重大的失误一般还是不会发生的。问题很可能出在一些没人注意到的小细节上。比如说，实验的时候用粉色的瓶子装新药，用蓝色的瓶子装安慰剂，然后让被试人从中随机选一个来用。结果呢，MM喜欢粉色，选的都是新药；男的呢则大多选择了蓝瓶子，用的都是安慰剂。最后，新药和安慰剂都发完了，因此直到结果出来之前没有人会注意到这个微小的性别差异所带来的统计失误。
    当然，上面这个药物实验的例子并不是真实的，一看就知道那个数据是凑出来方便大家计算的。不过，永远不要以为这种戏剧性的事件不会发生。一本叫做《致命的药物》的书详细披露了20世纪美国的一次重大药害事件，其原因可以归结到药物实验上去。药物实验的时间是有限的，如果用死亡率作为唯一标准的话，估计每个药物实验都得观察个十几二十年才行。为此，科学家们想到了利用各种“中间变量”来替代死亡率这一指标。

    统计数据表明，抑制心律失常能够减少死亡率，而当时的药物实验明确表明该药物能有效地抑制心律失常。这些药物得到了FDA批准并成功上市，当时每年有20多万人服用这些药品，超过5万人因为服用这种药物而死亡。这个药物实验中蕴含的逻辑推理看似无懈可击，到底什么地方出错了呢？人们推测很可能是某个第三方变量的问题。我们不妨称这种情况为“中间变量悖论”。

               抑制心律失常           死亡率
              对照组  实验组     未抑制    抑制
无缺陷(70%)    0.02    0.99       0.02     0.01
有缺陷(30%)    0.98    0.79       1.00     0.02
---------------------------------------------------
期望值         0.38    0.93       0.314    0.013

    让我们假设存在一个第三方因素，例如基因问题。我们不妨暂时管它叫做“先天缺陷”。从上表中我们可以看到，实验组（使用新药的人）中有93%的人成功抑制了心律失常，远远高于什么都不做的人(38%)；同时，心律失常确实会导致31.4%的人心脏骤停而死，但抑制心律失常则把这个比率下降到1.3%。这似乎确实可以说明，新药能够有效降低死亡率。但引入第三方因素后，情况有了很大的改变。有先天缺陷的人，心律往往很正常，恐怖的是一旦无法抑制心律失常则必死无疑。真正要命的就是，这种药物会使那些有先天缺陷的人心律变得更差。在没有缺陷的那70%的人当中，用药后有99%的人能抑制心律失常，而这里面只有1%的人会死；同时，另外1%的人则无法抑制，其中又有2%的人会死亡；有先天缺陷的那30%的人就惨了，用药后抑制住心律失常的人反而下降到79%，其中有2%的人会死，而对于另外21%的人则必死无疑。计算表明，使用药物后死亡的人数竟然三倍于不使用药物时的情况！

   (0.7*0.99*0.01 + 0.7*0.01*0.02 + 0.3*0.79*0.02 + 0.3*0.21*1.00)
/ (0.7*0.02*0.01 + 0.7*0.98*0.02 + 0.3*0.98*0.02 + 0.3*0.02*1.00)
≈ 2.91

    可以看到，从数据中挖掘因果关系并不是那么简单的事。如何确定影响目标的事件，如何从数据中获取相关关系，怎样用最少的实验次数（控制最少的变量）为因果关系定向，这都是建立一个因果网络所需要考虑的因素。因果网络是一个很复杂的学问，前天的讲座里还提到了很多确定因果网络的算法，在这里我就不再多说了。