2008-10-17 18:05| 
10 Comments | 本文内容遵从 你能想到的最大的数是多少？我电脑里A片的字节数？人体的细胞个数？整个地球的质量？宇宙间所有原子的个数？当然，在数学研究中，数学家们很可能会创造出一些比这些数都大的数。
1938年，数学家Edward Kasner的外甥发明了一个表示10^100的单词googol，这个数已经超过了宇宙中所有原子的个数。Pólya曾经猜想，小于等于n的正整数中，质因子个数为奇数的数不少于质因子个数为偶的数；1958年数学家C. B. Haselgrove首先给出了一个长达361位的反例。上个月，人们找到了一个新的Mersenne素数2^43112609-1，它一共有12978189位。1955年，数学家Stanley Skewes证明在不超过10^(10^(10^963))的范围内存在x满足π(x) > li(x)，其中π(x)表示不超过x的素数有多少个，而li(x)则是dt/ln(t)从0到x的定积分。
根据一项吉尼斯世界纪录，目前人类所创造的具有实际意义的最大的数是Graham数。
考虑这样一个问题：给定一个n维超立方体，连接这2^n个顶点所产生的所有点对，得到一个顶点数为2^n的完全图。对所有边进行红蓝二染色。是否可能找到某个n，使得在任意染色方案中总存在一个完全子图K_4，它的所有边都是一种颜色，并且四个顶点共面？我们通常把满足要求的最小的n记为N*。1971年，Graham和Rothschild证明了满足要求的n是存在的，并且给出N*的一个上界：N*<=g(64)，其中g(1)=3↑↑↑↑3，并且g(n)=3↑↑...↑3（共g(n-1)个“↑”）。“↑”是Knuth发明的一种数学符号，简单地说，它的定义如下：
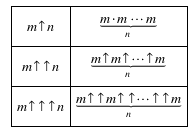
注意并列的“↑”要从右至左计算。因此，m↑n就表示m^n，而m↑↑3则表示m↑m↑m，即m^(m^m)。
通常把这个g(64)叫做Graham数。Graham数有多大呢？这恐怕只能靠诸位想象了。上面这句话没有任何修辞手法，因为我们真的无法用任何现有的语言直观地说明这个数的大小。即使说它有多少位，或者它的位数有多少位，或者我们需要在前面那句话里嵌套进多少个“的位数”（相当于用n^n^n^...^n的形式来表示），也不能言出这个数的大小。
以前你好像一直没提新发现梅森素数的事，今天终于提了一下
板凳
地毯
我在一本很小很小的册子上面见到过 ↑ 符号
没想到这还有记录
取几次对数的话
用↑↑表示的数貌似还是不大的了
↑↑↑还是无法想象的..
en.wikipedia.org
http://en.wikipedia.org/wiki/Big_numbers
上有很多介绍
我想还是办法基于N*再构建更大的具有一定意义的数的。
如果将宇宙年龄类比成自然数的无穷大，这个N*貌似已经可以被认为是阿列夫1了。
↑这个符号，一个的话就是指数级，两个的话还能在纸上描绘出来，也就是指数的指数的指数上去一共n层楼。可是到三个↑的时候，纸上已经无法描绘了，不过心里面还是能想的清楚的。到四个↑的时候彻底晕倒了，大脑也已经无法想象到底怎么计算m↑n了。
文中的N*竟然是用它的前面一个级数来表示↑有多少个！真佩服那些数学家，如何处理这种根本无法想象的数字的。
有谁能想象g(N*)是怎么样子的么，嘿嘿
googol
想起了Google的由来~
Rothschild
让我想起了货币战争上的某人
传说某家族又50万亿美元家产....