有时候，一个看似更加复杂的问题反而有一个更简单的解答。
    四色问题是说，对一个平面地图进行染色，要想用不同的颜色来区别相邻的区域，最少需要多少种颜色。在很长一段时间里，人们猜想，只要四种颜色就足够了；但这个“四色猜想”却怎么也证不出来。直到上世纪70年代，“四色猜想”才在计算机的帮助下获得证明。在《从一到无穷大》一书中，作者提到了这样一个有趣的事实：平面上的四色问题一直是一个相当复杂的难题，然而有意思的是，在环面上的染色问题却只需要短短十几行文字就能得出一个完美的结论。下面我们来说明，给一个游泳圈上任意划分出来的区域进行染色，为了使相邻区域不同色，只需要7种颜色就够了。
    为了证明这一点，我们只需要说明，在一个环面图中总能找到一块区域，它的邻域不超过6块。如果真是这样的话，余下的部分用数学归纳法就直接证到了：对于一个有n个区域的图，我们找出它的一个邻域数量不超过6的区域，然后把这块区域缩小为一个点，使整个图的区域个数减少到n-1。按照我们的数学归纳，这个有n-1个区域的图是可以7染色的；并且显然地，把第n个区域添加回去后所产生的图仍然可以7染色，因为我的邻域不超过6个，我总能找一个和这些邻域都不一样的颜色。
    现在的问题就是，为什么总存在邻域数量不超过6的区域呢？注意到在环面上，有V+F-E=0，其中V表示顶点数，F表示区域数，E表示边的总条数。注意到每个顶点都发射出了至少三条边，即所有顶点引出的边数至少为3V；但每条边都被重复计算了一次（因为一条边有两个端点），因此3V/2≤E，即3V≤2E。代入V+F-E=0，得到E≤3F。假设每个区域都有7个或7个以上的邻域，那么它们将产生至少7F条边；但每条边都被重复计算了一次（因为每条边都为两块区域共享），因此7F/2≤E，即7F≤2E。于是，2E≥7F>6F≥2E，矛盾。

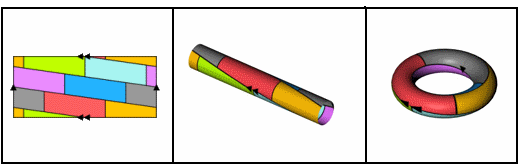
    事实上，7种颜色是必需的。构造一个至少需要7种颜色才能染色的环面是一件非常有趣的事情。其实，只要你想到了下面这一点，构造这样的环面是非常容易的：把游泳圈剪断并拉成一根空心的管子，再从中间破开来摊成一个长方形，所谓的“环面”实际上就是一个特殊的矩形平面区域——它的上下和左右是“通的”。下面这个图是从Wikipedia上找来的，它告诉了你如何制作一个7块区域两两相邻的环面。