UyHiP 趣题：能否把一个凸四边形分成若干个凹四边形

下面这个趣题出自 Using your Head is Permitted 谜题站 2016 年 10 月的题目：能否把一个凸四边形分成若干个凹四边形？

答案是否定的。我们给出一个非常漂亮的证明。在下面的文字中，我们用“优角”一词来表示一个大于 180 度小于 360 度的角。

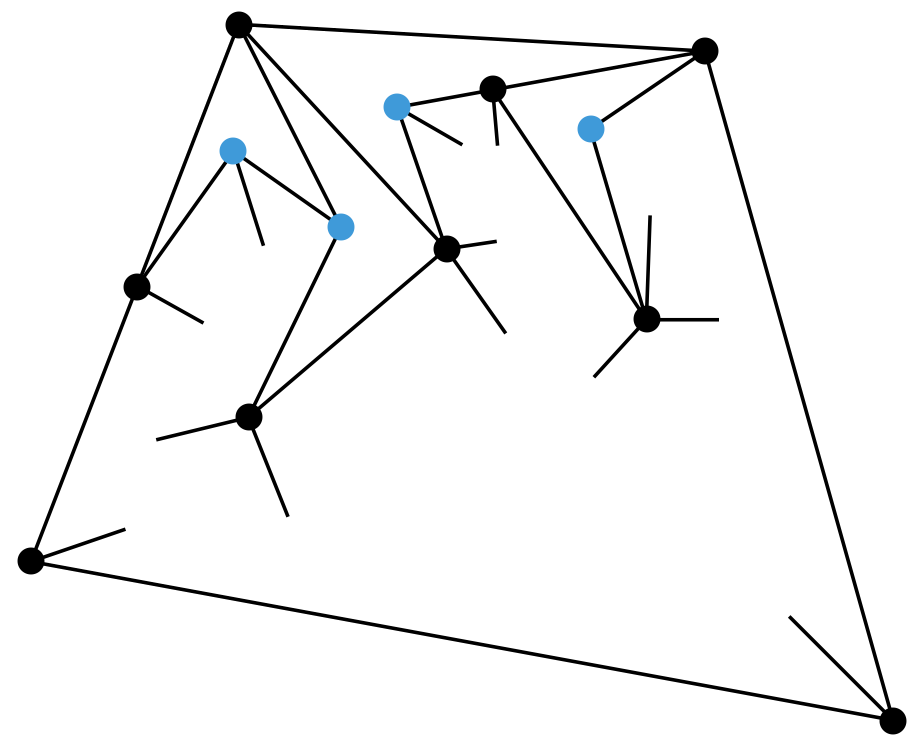
假设某个凸四边形被分成了若干个凹四边形。容易看出，每个凹四边形的内角中都有且仅有一个优角（如果没有优角，它就不是凹四边形；如果有两个或更多的优角，就与四边形内角和为 360 度矛盾）。

现在，让我们把每个凹四边形的那个优角顶点涂成蓝色。容易看出，每个蓝色顶点只能成为一个凹四边形的一个优角顶点（否则汇聚于该点处的角度之和会超过 360 度）。这意味着，每个蓝色顶点都唯一地对应一个凹四边形。如果图中的蓝色顶点一共有 n 个，那么凹四边形也一共有 n 个。

我们用两种不同的方式来统计所有凹四边形的所有内角的度数之和。汇集在每个蓝色顶点的内角之和都是 360° ，汇集在原四边形四个顶点处的内角之和也是一个 360° ，所以我们已经有至少 n × 360° + 360° 了。考虑到其他没涂成蓝色的顶点处还有很多角，因此上面这个数目实际上还会更多。但是，我们一共有 n 个凹四边形，每个凹四边形的内角之和是 360° ，因此所有凹四边形的所有内角之和显然应该是 n × 360° 。这个矛盾说明，我们无法把一个凸四边形分成若干个凹四边形。

55 条评论

发表评论




Enter Captcha Here :