2016 年 IMO 的第 6 题（也就是第二天比赛的第 3 题）非常有趣，这恐怕算得上是近十年来 IMO 的所有题目中最有趣的题目之一。平面上有 n ≥ 2 条线段，每两条线段都有一个交点，并且任意三条线段都不交于同一点。 Geoff 打算在每条线段的其中一个端点处放置一只青蛙，并让每只青蛙都朝向它所在线段的另一个端点。然后， Geoff 将会拍 n – 1 次手。每次拍手时，每只青蛙都立即向前跳到它所在线段的下一个交点处（青蛙们在跳跃过程中始终不会改变方向）。 Geoff 希望巧妙地安排初始时放置青蛙的方法，使得在整个过程中，任意两只青蛙都不会同时到达某个相同的交点。这个题目有两个小问。
- 证明：当 n 为奇数时， Geoff 一定有办法实现他的要求。
- 证明：当 n 为偶数时， Geoff 永远无法实现他的要求。
下图是 n = 5 时的其中一种可能的线段布局，以及其中一种满足要求的青蛙放法。你可以试一试， n = 5 时的其他放法就不见得满足要求了，而 n 为偶数时的任何一种放法都是不满足要求的。
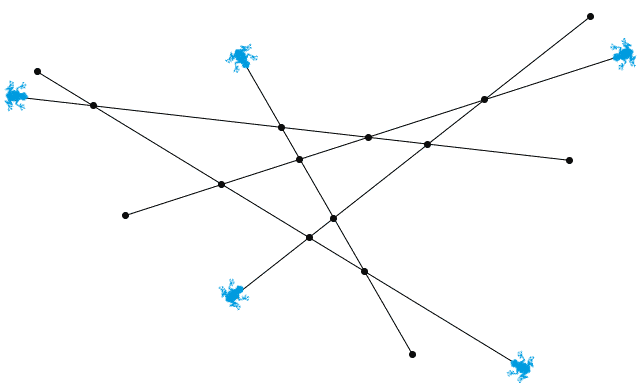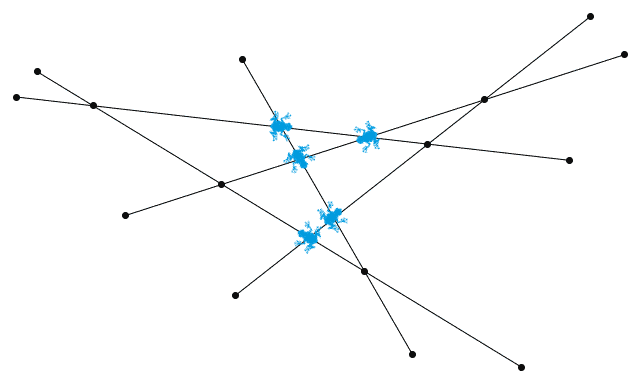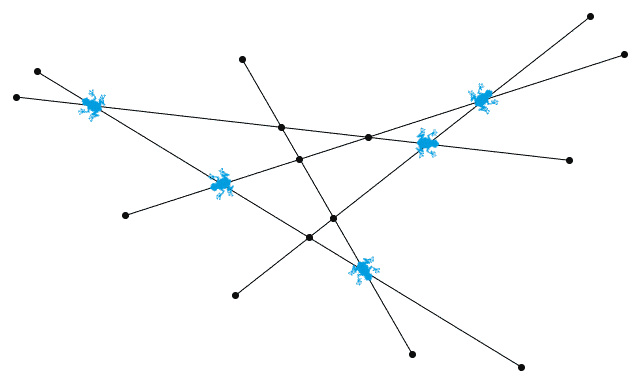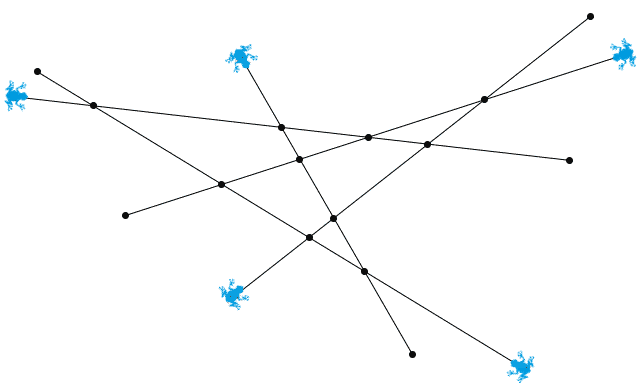
注意到，在上面这种满足要求的青蛙放法中，任何两只青蛙都不在“相邻”的端点上。这不是巧合。我们接下来说明，把两只青蛙放在“相邻”的端点上，则这两只青蛙必然会相撞。这里，我们可以为“相邻”下一个更加明确的定义。将所有线段充分延长，并与一个充分大的圆相交。把每条线段的端点都改到这些交点处，于是所有线段的所有端点就变为了一个圆周上的 2n 个点。如果两个端点之间的圆弧上没有其他端点，我们就说这两个端点是相邻的。
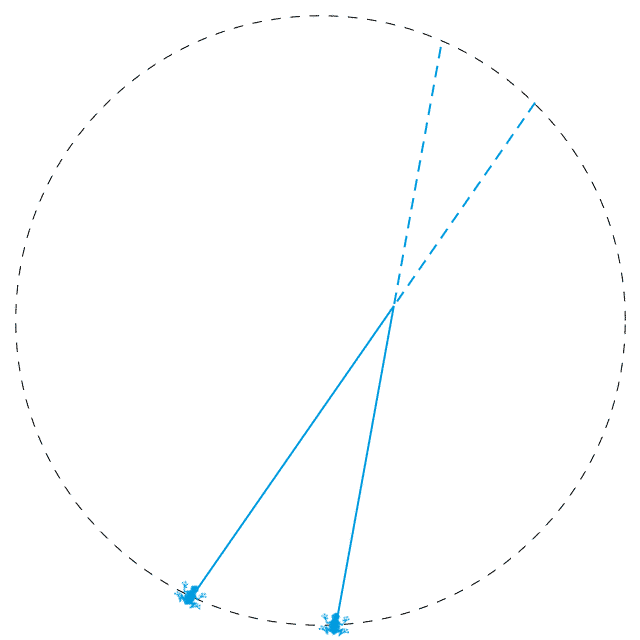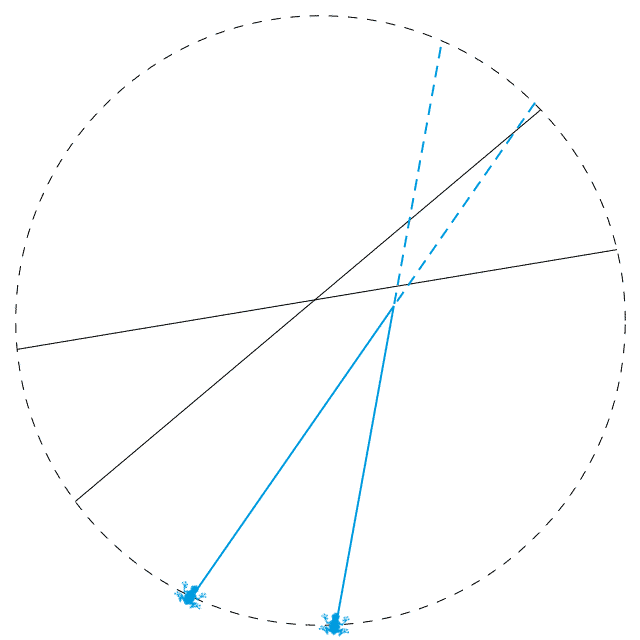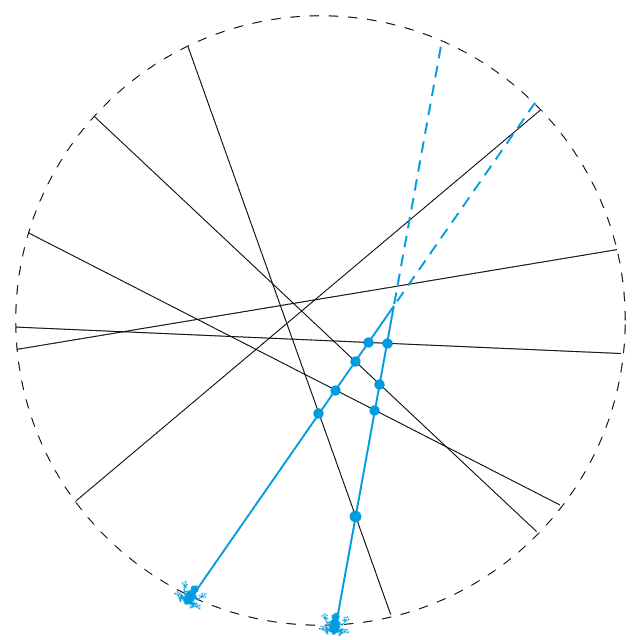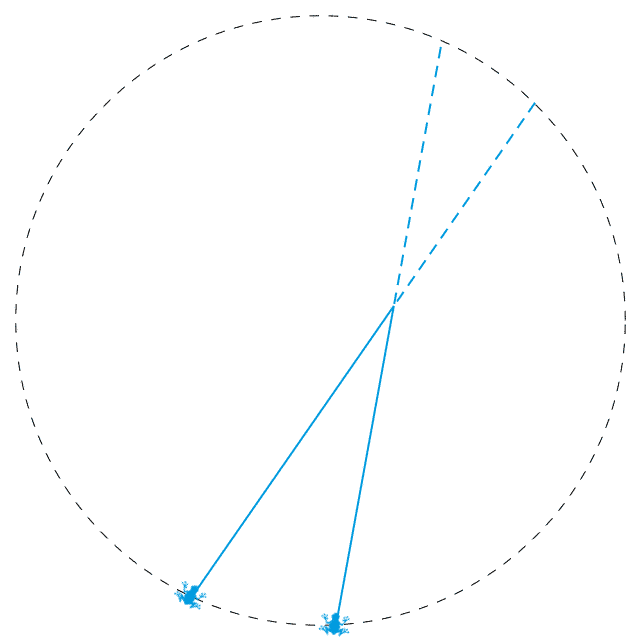
现在，假设我们把两只青蛙放在了两个相邻的端点上，如上图所示。蓝色的线表示的就是这两只青蛙所走的路，其中实线部分表示这两条路相交前的部分。由于两个端点是相邻的，因此这两条蓝线之间不再夹着其他线段。所有其他线段都是横穿过这两条蓝线的，它们与两条蓝线的交点要么都在虚线部分，要么都在实线部分。这会使得两条蓝色实线上产生出相同数目的交点。于是，两只青蛙将会同时到达两条蓝线的交点处。
这就说明，把两只青蛙放在相邻的端点上是必死的。在一个满足要求的放法中，任何两只青蛙中间都要间隔至少 1 个端点。然而，我们一共有 n 只青蛙和 2n 个端点，因而这些青蛙必须得恰好每隔 1 个端点放一只。考虑到这一点，我们立即就把第 2 小问解决了。当 n 为偶数时，对于任意一条线段，都有 n – 1 条线段穿过它，这意味着这条线段的两个端点之间恰好隔着 n – 1 个端点（不管是算哪边的弧），这是一个奇数。所以，如果每隔 1 个端点放一只青蛙，那么这条线段的其中一端放了青蛙，另外一端也会有只青蛙。这是不符合要求的。
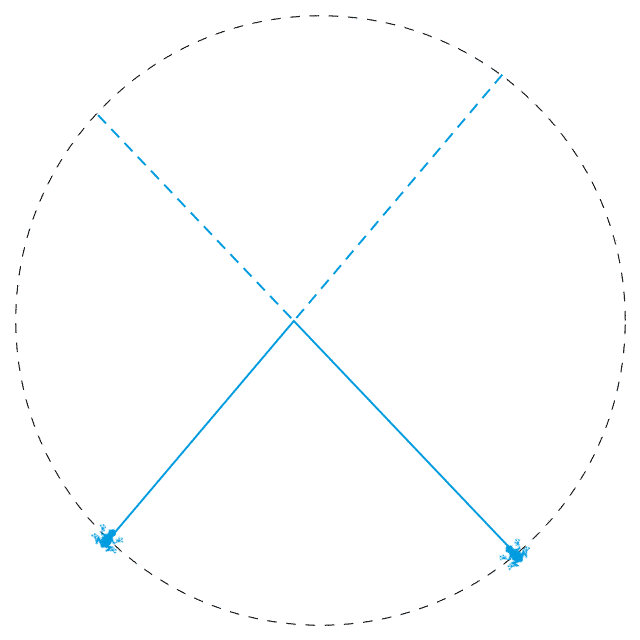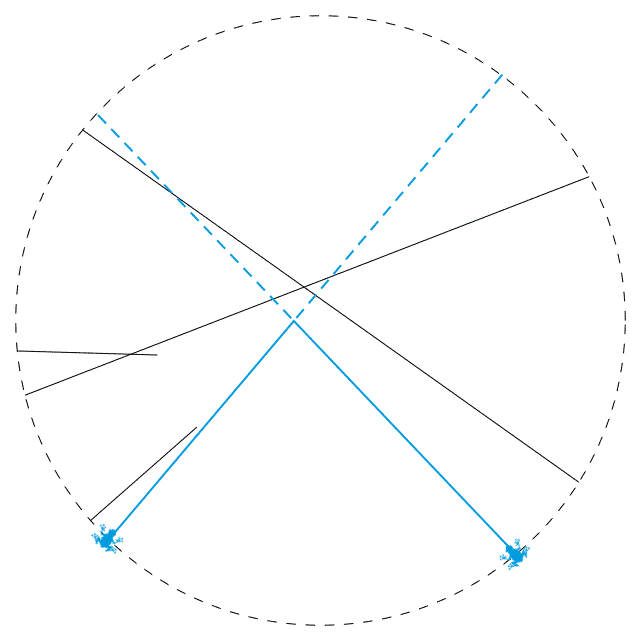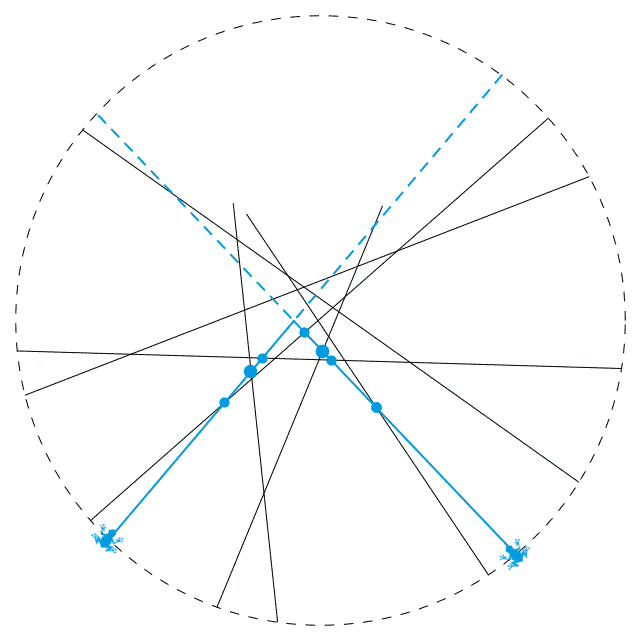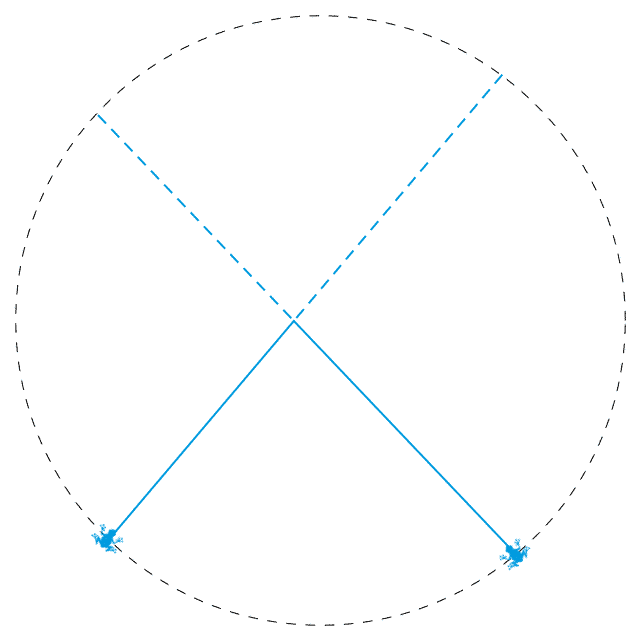
而当 n 为奇数时，每隔 1 个端点放一只青蛙，就会正好让每条线段上都有一只青蛙。容易看出，此时任意两只青蛙之间都会隔着奇数个端点。接下来，我们证明，只要两只青蛙之间隔着奇数个端点，那么这两只青蛙一定不会相撞。如上图所示，我们还是用蓝色的线表示这两只青蛙所走的路。其他的线段分成这样三类：
- 从虚线处横穿过这两条蓝线
- 从实线处横穿过这两条蓝线
- 夹在这两条蓝线之间
根据刚才的讨论，第一种类型的线段不会在两条蓝色实线上产生交点，第二种类型的线段会在两条蓝色实线上产生相同数目的交点。至于第三种类型的线段，每一条要么与这边的蓝色实线相交，要么与那边的蓝色实线相交。由于两只青蛙之间隔着奇数个端点，因此这种类型的线段有奇数条，在这边的蓝色实线产生的交点数与在那边的蓝色实线产生的交点数就必然是一奇一偶。综合这三种类型的线段，我们最终得出，这些线段在两条蓝色实线上产生的交点数目是不同的，因为数目的奇偶性都不一样。所以，两只青蛙不会相撞。
回想我们刚才所说的，当 n 为奇数时，间隔着放青蛙会使得每条线段上都各有一只青蛙，并且任意两只青蛙之间都会隔着奇数个端点。这就将成为一种满足要求的放法。于是，我们就完整地证明了第 1 小问的结论，整个问题也就解决了。
这道题背后有一个有趣的故事。现任 IMO 主席 Geoff Smith 赛前曾经说，他将会以一种特殊的形式与参赛选手互动。最终，谜底揭晓：他成为了 IMO 第 6 题的主人公。
啊，沙发
有点儿好奇，请问这个图是用什么软件画的？
= =
@livc 你回复的回复不偏离主题？-V-
我什么总有人关注画图软件。。完全偏离主题。。
你这个回复不偏离主题？
终于有一道IMO题能看懂答案了(- -;)
这题可以有，话说动图是怎么做的?
動圖應該是用Mathematica製作出來的
在http://www.matrix67.com/blog/archives/6231有提到
哎，组合题都是些看得懂答案，自己做做不出来的坑爹货..
很喜欢这种题目，当年参加联赛的时候，有道题目是五子棋，也是有的的很。只可惜，进入冬令营后，木有进入imo。
求助 matrix67 大牛一个博弈问题：
有编号1~n的石头，两个人轮流取，取最后一个石头为输。
一次取1个石头或者2个编号连续的石头（如果k石头不存在，取k-1和k+1号石头不合法）。
问，n等于多少后手必赢。
我拿程序跑了n=70的所有情况也都是先手必赢。但是证明不了。
求大牛帮忙解答，或者转给其他大牛。非常感谢！
如果愿意拨冗交流，欢迎给我邮件orQQ。
联系方式：602546990@qq.com
上面的描述部分因为大于小于号，被吞了，我下面重新写一个。
n=4的时候就是后手必胜啊
求助 matrix67 大牛一个博弈问题：
有编号1~n的石头，两个人轮流取，取最后一个石头为输。
一次取1个石头或者2个编号连续的石头（如果k石头不存在，取k-1和k+1号石头不合法）。
问，n等于多少后手必赢。
我拿程序跑了n小于70的所有情况，只有n=1,4,9,12,20 这5个值是后手必赢，其他都是先手必赢。
我猜想是不是n大于等于70的所有情况也都是先手必赢。但是证明不了。
求大牛帮忙解答，或者转给其他大牛。非常感谢！
如果愿意拨冗交流，欢迎给我邮件orQQ。602546990@qq.com
md才看到这里改过了。
由于涉及到一个胜负转换的问题，你这个问题还需要考虑必败策略，也就是一定能取到最后一枚石子的策略。综合起来也许能覆盖所有情况，得到证明。
……不管n是多少都是先手有必败策略。我再想一下……
这个题没有那么复杂呢，如果取得n的人输，想赢的人必须取得n-1。后手有控制比赛进程的方法，即先手取得1，后手取得2；先手取得2，后手取得1，以保证整个进程以3的倍数进行。若n=100，后手应取得99，即3,6,9,12…93,96,99，先手必输。若n=99，后手应取得98，即2,5,8…92,95,98。但当先手第一次取得2后，两人状态互换，先手必胜。同理可证n=97的类似情况。所以胜负应是交替出现的，不止是n=1,4,9,12,20 几个情况
话说你有没有想过把博客上的内容做成一个微信公众号？
I hate my life but at least this makes it berblaae.
以前还专门训练过这种类落点的问题，当时是棋盘，确实很好玩
IMO蛤?
IMO蛤。。。
顾老师，我是您四年前的学生😄可是我为什么无法关注您的站点呢？
老师您好，可以做一个文章列表吗？方便查看以往文章
有趣
蛤蛤
文章很好，，，，
文章很好，，，
如果能讲一下题目的来源，或者背后的应用就更好了。看了n=5的动图，感觉跟譬如飞机航线规划之类的问题有关系。
test
First name:
Last name:
Submit
Reset
alert(‘aa’)
呵呵
Please update your blog.
您好！有个生物数学问题请教。我在研究颗石藻，颗石藻是单细胞球形，分泌一种碳酸钙晶体，晶体是一个椭圆环状结构，每个细胞由6-30个晶体相互嵌合，把每个晶体当多边形处理，那么细胞就是个多面体，可以用euler公式。我观察到多边形的边为4-6，我能解释为什么不能有三边形，但解释不了为什么不能有7边形。有文献说7边形会betray negative curvature，而4和5边形betray positive curvature。怎么理解，能用来解释吗？另外，二维平面上，有个lewis’s law，即多边形的边越多面积越大。多面体也有类似规律吗？感觉阿基米德多面体就是。方便的话，QQ5144161或者邮箱kaixu@jmu.edu.cn联系。
求您了更新吧
“所有其他线段都是横穿过这两条蓝线的，它们与两条蓝线的交点要么都在虚线部分，要么都在实线部分”
为什么没有可能一条是在虚线部分另一条是在实线部分
alert(“Hello World”);
你们的博客好有爱，
这个评论系统是内建的嘛
第一次看，没看太明白
好些年没更新了
wow 竟然也有人在看
牛人一个。
求老师复出
第一题可以用数学归纳法解答，绕过一切内部规律的认知
在n=3的情况下，不难给出可行方案（略）；
假设n=a的情况下，有可行方案；
那么n=a+2的情况下，可采用如下步骤迭代到新方案：
1.保留n=a的拓扑结构，将原线段延伸至足够长，视野缩放到足够远，所有原线段尽量压缩至水平方向
2.在远离原交点群的左侧，尽量垂直部署第a+1条线段；
在远离原交点群的右侧，尽量垂直部署第a+2条线段；
新增的两条线段相交于原交点群上方较远处
3.将a+1号青蛙出生点置于上方，a+2号青蛙出生点置于下方（需确保a+1号线段左下临近老端点必须是出生点位、a+2号线段右下临侧的老端点不能是出生点位，如不符合条件可旋转原方案）
在新方案中1～a号青蛙的第一跳与最后一跳必然落在a+1号与a+2号条线段上，中间步骤全部复用老方案，因此1～a号青蛙相互间无碰撞；另外不难证明，a+1、a+2号青蛙无碰撞；1～a号青蛙分别与a+1、a+2号青蛙无碰撞；因此n=a+2方案成立。