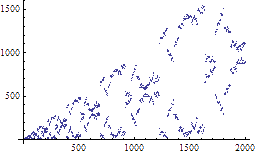
Daisuke Minematsu和他的同学们发现，Josephus问题中也隐藏着分形图形。Josephus问题是初学编程的人必然会接触到的一个问题——n个人围成一圈进行1到k报数，每次报到k的人退出游戏（离开这个圆圈），那么最后剩下的那个人是谁。在这里，我们考虑一个Josephus问题的变种：双向Josephus问题。双向Josephus问题中有两个交替进行的报数进程，其中一个按顺时针方向踢出每第k个人，另一个进程则逆时针踢出每第k个人。两个进程交替进行，直到最后只剩一人为止。假如n=10, k=3的话，第一个退出的人是#3，第二个退出的人是#8，第三个退出的人是#6，以后分别是4, 10, 9, 5, 1, 7，最后剩下的人是2。我们用S(n,k)来表示在相应的n值和k值的情况下最后剩下的那个人的编号，对于每个固定的k值，函数S的图象竟然都是一个分形图形。右图是S(n,4)所对应的图象，你可以非常清楚地看到这个图象的自相似性。你可以自己用Mathematica来验证一下。

joseprocess[m_, mm_] := Block[{t, p, q, u, v, w},
   proc = {}; w = mm; t = Range[m]; p = t; q = t;
   Do[p = RotateLeft[p, w];
      u = First[p]; proc = Append[proc, u];
      p = Rest[p]; q = Drop[q, Position[q, u][[1]]];
      If[Length[p] == 1, Break[]];
      q = RotateRight[q, w];
      v = Last[q]; proc = Append[proc, v];
      q = Drop[q, -1]; p = Drop[p, Position[p, v][[1]]];
      If[Length[q] == 1, Break[]],
    {n, 1, Ceiling[m/2]}];
   proc];
 
ListPlot[Table[Complement[Range[n], joseprocess[n, 3]][[1]], {n, 2, 1000}]]

参考资料：http://demonstrations.wolfram.com/TheJosephusProblemInBothDirections/