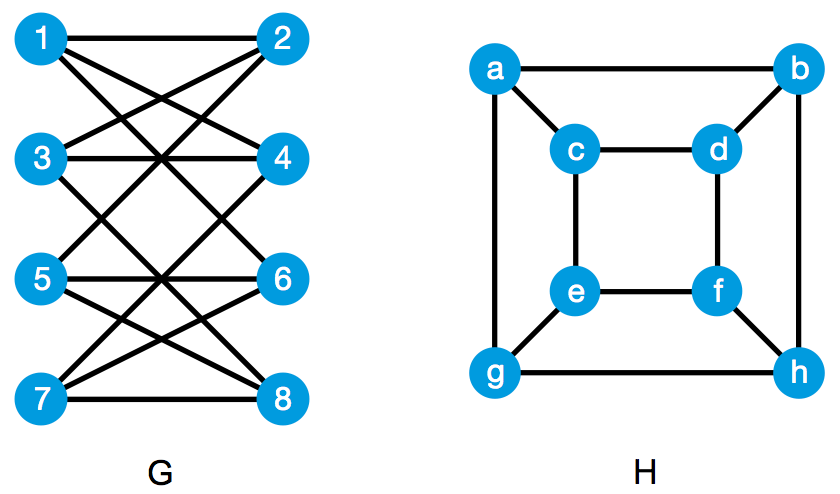
若干个顶点（vertex）以及某些顶点对之间的边（edge）就构成了一个图（graph）。如果图 G 和图 H 的顶点数相同，并且它们的顶点之间存在着某种对应关系，使得图 G 中的两个顶点之间有边，当且仅当图 H 中的两个对应顶点之间有边，我们就说图 G 和图 H 是同构的（isomorphism）。直观地说，两个图是同构的，意思就是它们本质上是同一个图，虽然具体的画法可能不一样。下面的两个图就是同构的。其中一种顶点对应关系是： 1 – a, 2 – c, 3 – d, 4 – b, 5 – e, 6 – g, 7 – h, 8 – f 。
目前，人们还没有找到任何高效的算法，能迅速判断出两个图是否同构。在普通计算机上，判断两个图是否同构，这需要花费大量的时间。因此，人们经常以图的同构为例，来解释复杂度理论和现代密码学中的诸多概念。
假设你家里的计算机十分强大，能很快判断出两个图是否同构，还能在两个图确实同构的情况下，给出一种顶点对应关系。但你的同桌家里的计算机却非常弱，没法做什么大型运算。课堂上，老师向全班展示了两个很复杂的图，不妨把它们叫作图 G 和图 H 。老师布置了一个特别的选做题：判断出这两个图是否同构。每个同学都可以提交答案，答案里只需要写“是”或者“不是”即可。按时提交答案并答对者，期末考试会获得 5 分加分；按时提交答案但答错了的，期末考试成绩将会倒扣 30 分；不参与此活动的同学，期末考试既不加分也不扣分。显然，每个同学都不敢随意提交答案，除非百分之百地能保证自己获得的答案是正确的。回到家后，借助家里的超级计算机，你很快判断出了这两个图是同构的。你给你的同桌发送了信息：“我已经算出来了，这两个图是同构的。”但是，你的同桌却回复说：“你不会是骗我的吧？”你打算怎样说服他，这两个图确实是同构的呢？
你只需要把两个图的顶点对应关系发送给他即可。他家里的计算机非常弱，没法找出满足要求的顶点对应关系。但若有了一个顶点对应关系，验证其确实满足要求，这是非常容易的，几乎不需要什么计算量——只需要枚举图 G 里的顶点对，看看它们之间有边是否当且仅当图 H 中的对应顶点之间有边即可。完成验证之后，他就知道了，这两个图确实是同构的。
总结起来，刚才我们面对的是这样的困境：
- 你拥有无限的计算能力。
- 对方的计算能力非常有限。
- 你想要向对方证明，图 G 和图 H 确实是同构的。
判断两个图是否同构可能很难，但若给出一段证据后，很容易验证两个图确实同构，上述困境也就得以解决了。这就是复杂度理论中 NP 问题的大致意思。
但是，如果把两个图同构的证据直接交给你的同桌，你的同桌或许又会用同样的办法去帮助别人，最后搞得班上所有人都获得了加分，这就没意思了。有没有办法说服你的同桌，这两个图确实是同构的，但却又让他无法拿到这两个图同构的证据呢？也就是说，现在我们面对的是这样的困境：
- 你拥有无限的计算能力。
- 对方的计算能力非常有限。
- 你想要向对方证明，图 G 和图 H 确实是同构的。
- 你不想泄露这两个图的顶点之间的对应关系。
这看上去似乎是不可能实现的——不把顶点之间的对应关系告诉对方，怎样说服对方两个图确实是同构的呢？然而，这竟然是能做到的。整个过程分为很多轮进行。在每一轮里，你随机生成一个与图 G 同构的图 G′ 。如果图 G 和图 H 真的同构，那显然图 G′ 也与图 H 同构。然后，你把图 G′ 发送给对方。对方可以随机提出下面两个要求之一：提供 G′ 与 G 同构的证据，或者提供 G′ 与 H 同构的证据。不管对方提出的是哪个要求，你都可以放心大胆地把证据发给对方，这不会泄露图 G 和图 H 之间的对应关系。另外，如果图 G 和图 H 不是同构的，那么这两个要求你不可能都做得到；面对对方的抽查，总能如约作答的概率是很低很低的。很多轮过去后，对方便慢慢确信，图 G 和图 H 真的是同构的了。在现代密码学中，让对方相信命题的正确性，但又不泄露任何其他的信息，这就叫作“零知识证明”（zero-knowledge proof）。
现在，让我们再来看一种情境。去掉上述第四点要求，但把第三点要求改一下：
- 你拥有无限的计算能力。
- 对方的计算能力非常有限。
- 你想要向对方证明，图 G 和图 H 确实是不同构的。
你打算怎么办？注意，你的办法应该普遍适用于一切情况。在某些特定的情况下，你当然可以告诉对方，“这两个图显然不同构，因为它们的边数就不一样多”，但这不适用于两个图的边数一样多的情况。
很简单。每次让对方随机生成一个与图 G 同构的图或者与图 H 同构的图，并把它发送给你。每次你都可以准确地告诉对方，刚才发来的图是从图 G 变过来的，还是从图 H 变过来的。多试几次，对方便能确信，这两个图确实是不一样的。
上述所有例子都属于“交互式证明”（interactive proof）。第一个例子是确定性的交互式证明（deterministic interactive proof）。它也是最简单的一类交互式证明。第二个例子则是带有附加条件的交互式证明。也就是说，零知识证明是一种特殊的交互式证明。第三个例子则表明，对于有些问题来说，交互式证明的存在性并不是显然的（即使没有任何附加条件）。如果利用确定性的交互式证明，你能向别人说明问题的答案是肯定的，我们就说这个问题属于 dIP 集合。很容易证明， dIP = NP 。如果利用交互式证明（包括非确定性的交互式证明），你能向别人说明问题的答案是肯定的，我们就说这个问题属于 IP 集合。交互式证明理论的一个最主要的结论就是 IP = PSPACE ，其中 PSPACE 表示所有能用多项式的空间解决的问题。
第一个例子和第二个例子都是我早已听说过的例子。第三个例子以及与此相关的交互式证明理论则是我最近在 Introduction to the Theory of Computation 一书中看到的。它们应该都是复杂度理论中非常经典的例子。
第一次做沙发，先mark了
第三个例子，如果G和H其实是同构的：
每次让对方随机生成一个与图 G 同构的图或者与图 H 同构的图（于是这个新图总是既和G同构，也和H同构），并把它发送给你。每次你都可以准确地告诉对方，刚才发来的图是从图 G 变过来的，还是从图 H 变过来的（无论说哪个都是正确的）。
于是还是无法证明G和H不同构？
注意前提条件是你要向对方证明G和H不同构，所以你说的这个情况其实不需要考虑。
退一步说，如果G与H同构，对方生成一个与G同构的图F，则你无法判断F到底是由G还是H生成的。一旦你的回答错误，对方就知道G和H其实同构，或者你在骗他。
既然同构了怎么可能知道图 G 变过来还是图 H 变过来？
你脑子没事吧？
前提是对方测试：我说G,H不同构，是不是在骗人。。。对方做了个G同构的图过来，如果我骗人，实际上G,H同构，则我有可能回复是H同构的，那就被发现我骗人了。。。
hillson正解
hillson：
”前提是对方测试：我说G,H不同构，是不是在骗人。。。对方做了个G同构的图过来，如果我骗人，实际上G,H同构，则我有可能回复是H同构的，那就被发现我骗人了。。。“
实际上G,H同构，则我不可能回复是H同构的吧。。。
AM和MA，非常有意思的内容。我们老师当时举的例子是说服色盲粉笔颜色。
什么题什么题 说来听听吧
好吧 我自问自答，就是只要这个色盲每次问别人粉笔的颜色 每次问的结果都一样 那命题就是肯定的。我理解的zero knowlege proof就是：尝试通过N次一致的结果证明这个命题是肯定的。
但是我觉得这个色盲问题其实不能体现交互式证明这个概念
一直没看回复，是这样的。
有一个盲人，有两支粉笔，然后有一个人需要说服他两支粉笔颜色不同。
盲人先用粉笔在黑板上画一个圆，如果两支粉笔颜色不同，另一个人一定可以每次都说对是哪支粉笔画的，否则另一个人不会有高于1/2的几率猜对
零知识证明那个，把证明过程记录下来给别的同学看就好。他们也只需要证明不需要知识呀。
+1
注意 证明过程中
对方可以随机提出下面两个要求之一：提供 G′ 与 G 同构的证据，或者提供 G′ 与 H 同构的证据。
如果不具有计算能力的话，是无法满足这个要求的，因为只知道其中一个。
“交互式证明”的“证明过程”不同于经典的“证明过程”。比如说我是原文中的“同桌”，我不知道正确答案，但是我可以自问自答、编几个回合的“证明过程”给“其他同学”看，“其他同学”不就被骗了嘛。
“把证明过程记录下来”的方法中，假定了同桌是诚实的。如果同桌跟“我”演双簧，一起骗其他同学的钱，那这个证明记录就不可靠了。零知识交互式证明中，最有价值的信息是“交互事件发生的顺序”。可靠的顺序是：“我”先发送同构图，同桌再生成随机数；如果双方串通，同桌先生成随机数，“我”再发同构图，那就可以伪造一份证明记录了。“事件发生的顺序”只有当事人和“上帝”知道，不在场的人是无法确认的，这就是为什么“交互”那么重要。
顾老师，能告诉我们为什么那么久没更新吗？
1. GI 问题的 zero-knowledge proof 已经属于 IP 而不是 dIP 了，因为 verifier 已经是 probabilistic；
2. dIP 与 IP 的区别不在于答案的肯定性，在于 verifier 是 probabilistic 以及允许 verifier 得到错误的结论。
“交互式证明理论的一个最主要的结论就是 IP = PSPACE ，其中 PSPACE 表示所有能用多项式的空间解决的问题。”
比如问a! mod b的奇偶性，这是PSPACE吧，那怎么是IP了，即利用交互式证明（包括非确定性的交互式证明），你能向别人说明问题的答案是肯定的
At last, soomnee comes up with the “right” answer!
思路是将问题规约为 TQBF（全量词化的布尔公式的真假性问题），后者属于 IP。
有生之年终于看到更新了……
终于更新了，还以为你怎么了
放假趣味读物 这博客真的很棒
M67，Pi节Conway发的那三道题求解答啊，尤其是最后一道
找您不太容易噢，我看了你的演讲 唉，这个教育，里面一个例子，农药残留高于国家标准，里面说改成农药残留严于国标 ，但农残标准是规定的最低标准啊，所以只要符合国标的都严于国标，严于等于通过或符合，我觉得都有点过度宣传，臭不要脸了。，甚至欺骗。
最近居然如此频繁的更新…
算晕了，算术不好
零知识证明哟
第三个例子，我想到的办法：
生成明显不同构的G’和H’（肉眼或弱计算机能识别）发给对方，对方随机要求证明其中哪个是G（或H）的同构，但不证明另一个；多次之后，对方相信G和H不同构。
修正一下：明确告诉对方G’是G的同构，H’是H的同构，但只按对方要求证明其中的一对
如果不用图这种纯数学的表述，这道题可以改为克隆同胞证明，验证一次就克隆一个
G和G’同构，则G’和H也同构。那么如果同学能够判断其中一组是同构的，而你又告诉他另外一组的对应关系，那么G和H的对应关系不就直接出来了吗？
G’和G、H一样复杂啊，你怎么知道同桌的计算机强大得能算出来?