下面这道题目是 Using your Head is Permitted 谜题站 2015 年 12 月的题目。

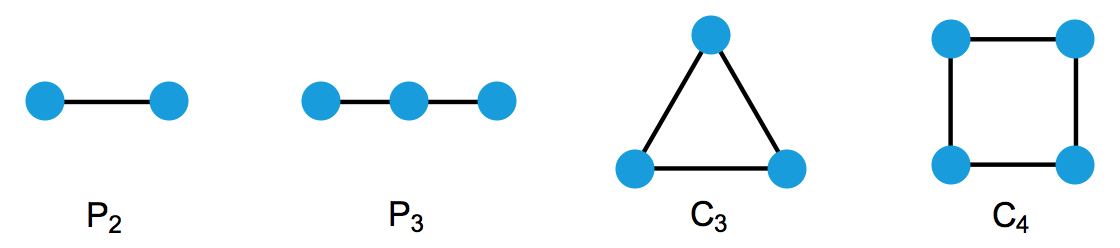
若干个顶点（vertex）以及某些顶点对之间的边（edge）就构成了一个图（graph）。下面就是这篇文章里会用到的四个图。其中，第一个图是由 2 个顶点组成的路径（path），因而我们把它称作 P₂ ；第二个图是由 3 个顶点组成的路径，因而我们把它称作 P₃ 。第三个图是由 3 个顶点组成的一个环（cycle），因而我们把它称作 C₃ ；第四个图是由 4 个顶点组成的一个环，因而我们把它称作 C₄ 。

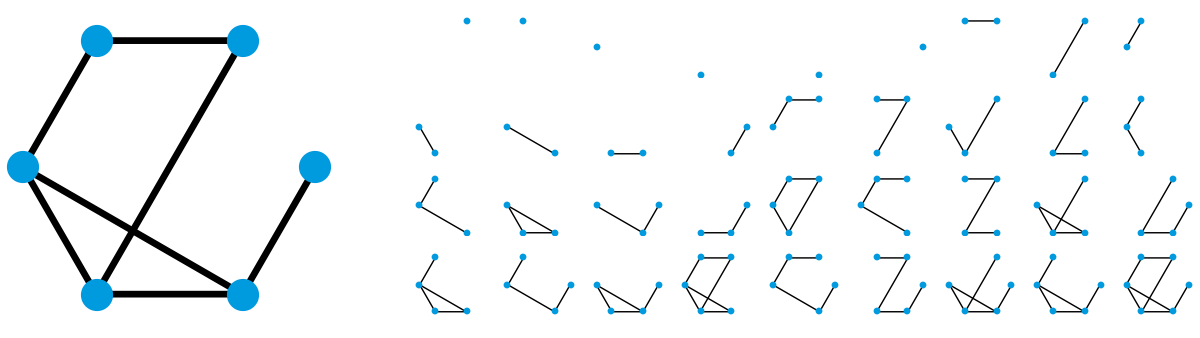
选取图中的一个或多个顶点，同时选出这些顶点之间的所有边，得到的就是原图的一个“诱导子图”（induced subgraph）。在这篇文章中，我们只考虑那些连通的诱导子图。下面是一个有 6 个顶点的图，右边则列出了由它可以产生出来的所有连通诱导子图。注意，由于有些诱导子图不是连通的（比如只选择正上方的两个点和右下角的两个点，或者干脆只选择最左边那个点和最右边那个点），因而它们并没有在右边列出。在这些连通诱导子图里，很多图的本质都是相同的。比方说，第一行最后三个图和第二行前面四个图的本质是一样的，它们都是刚才我们介绍过的 P₂ 。当然，第一行的前六个图的本质也都是一样的，即由单个顶点构成的图，有时会被人们记作 K₁ 。观察最后一行的倒数第二个和倒数第三个图，你能看出这两个图的本质也一样吗？只不过，它们就没有什么固定的名字了。在这些连通诱导子图里，哪一种图出现的次数最多呢？答案就是 P₃ ，它一共出现了 8 次。

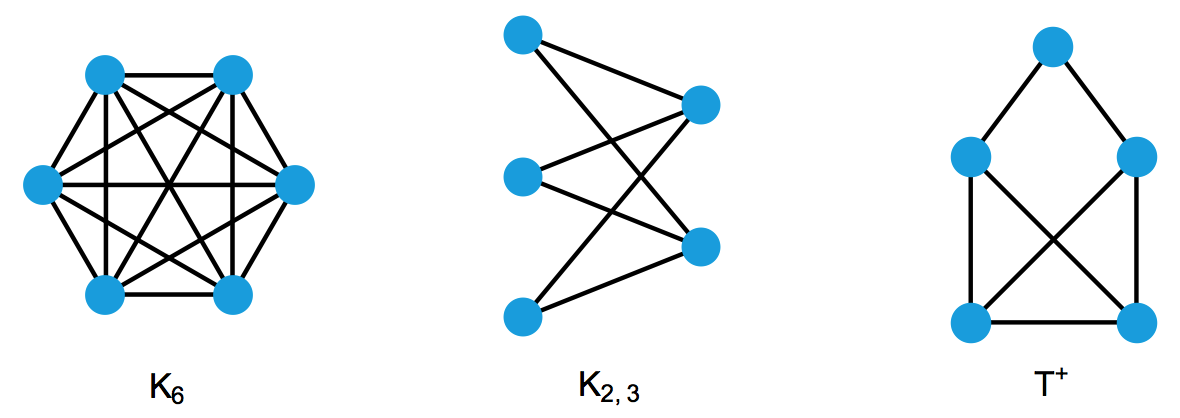
我们的问题是：能否构造一个图，使得里面出现次数最多的连通诱导子图是 C₃ ？能否构造一个图，使得里面出现次数最多的连通诱导子图是 C₄ ？注意，如果两种连通诱导子图出现的次数一样多，那它们都不算出现次数最多的连通诱导子图。

 

 

 

 

 

最左边的那个名叫 K₆ 的图显然满足， C₃ 是里面出现次数最多的连通诱导子图。这是因为，从 K₆ 中任意选出 3 个顶点，得到的诱导子图都是 C₃ ；同时，由对称性可知，当 n 为任意一个 1 到 6 之间的固定整数时，从 K₆ 中随便选出 n 个顶点，得到的诱导子图都是本质相同的。而 C(6, 3) 比其他 C(6, n) 的值都更大，因而 C₃ 的出现次数最多。

下面我们证明， C₄ 不可能成为某个图里出现次数最多的连通诱导子图。假设这样的图真的是存在的，不妨把它叫作图 G 。让我们用 P(G) 来表示图 G 中的所有形如 P₃ 的诱导子图所构成的集合。对于 P(G) 里的每一个图 x ，让我们用 S(x) 来表示，在图 G 里再选一个顶点加入 x 中，就能把 x 扩展成一个形如 C₄ 的诱导子图，这一共有多少种不同的方法。最后，我们用 X_i 来表示，在 P(G) 里有多少个 x 会使得 S(x) = i 。利用这些记号，我们就可以表达出诱导子图 C₄ 的数量了：

#(C₄) = Σ_i X_i · i / 4

式子中除以 4 的原因是，每个诱导子图 C₄ 都可以用 4 种不同的方法看作是由某个 P₃ 扩展而来的，因而每个诱导子图 C₄ 都被重复算了 4 次。

同时，我们还能表达出其他诱导子图的数量。例如，诱导子图 P₃ 的数量直接就等于

#(P₃) = Σ_i X_i

另外，对于 P(G) 里的每一个 x ，选出任意两种不同的扩展成 C₄ 的方案，并把这两种方案合并起来，我们就能得到一个有 5 个顶点的诱导子图。由于所选的两个新顶点之间有可能有一条边，也有可能没有边，因而这个诱导子图有可能是 K_{2, 3} ，也有可能是 T⁺ 。于是，我们有：

3 #(K_{2, 3}) + #(T⁺) = Σ_i X_i · i (i – 1) / 2

其中， i (i – 1) / 2 表示从 i 个元素里选出 2 个的方案数。 #(K_{2, 3}) 的前面有个系数 3 ，这也是因为每个 K_{2, 3} 都会被重复计算 3 次。

好了，现在考虑下面这个式子：

  #(C₄) – (0.5 #(P₃) + 0.375 #(K_{2, 3}) + 0.125 #(T⁺))
= Σ_i X_i (i / 4 – (1 / 2 + i (i – 1) / 16))
= Σ_i X_i (- i² / 16 + 5 i / 16 – 1 / 2)

这个式子相当于是用 C₄ 的数量减去 P₃ 、 K_{2, 3} 和 T⁺ 的加权平均数量（并且三者的权重之和为 1 ）。如果 C₄ 真的是出现次数最多的连通诱导子图，那么这个式子的结果应该是正的。但是， – i² / 16 + 5 i / 16 – 1 / 2 = – (1 / 16) (i – 5 / 2)² – 7 / 64 恒为负数，因此这个式子的结果应该是负的。于是产生了矛盾。

 

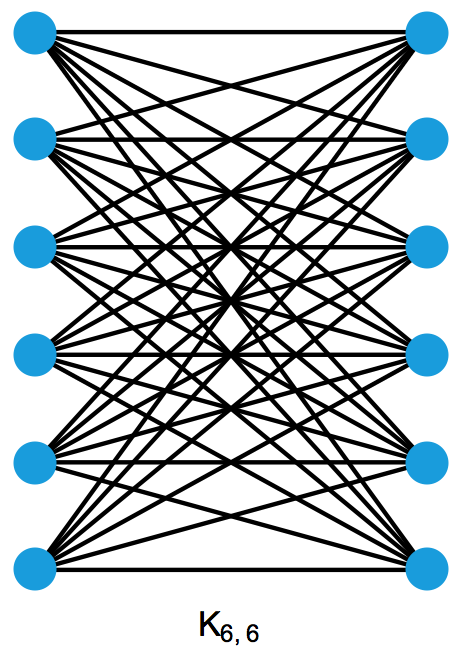
我们采用了颇有些曲折的办法，最终证明了，在任何一个图的所有连通诱导子图当中， P₃ 、 K_{2, 3} 和 T⁺ 里面至少有一样出现得比 C₄ 更多。为什么我们不直接去证明，在任何一个图的所有连通诱导子图当中，某种图 H 的出现次数总会大于等于 C₄ 出现的次数呢？原因很简单：因为这样的图 H 根本不存在。考虑 G₁ = C₄ ， G₂ = K_{6, 6} ，其中 K_{6, 6} 代表一个由 12 个顶点构成的图，所有顶点平分为左右两组，左边的每个顶点和右边的每个顶点之间都有一条边。在 G₁ 的所有连通诱导子图当中，出现次数能和 C₄ 相比的只有 K₁ 、 P₂ 和 P₃ （它们也就是 G₁ 中除了 C₄ 本身外其余的所有连通诱导子图）。但在 G₂ 的所有连通诱导子图当中， K₁ 、 P₂ 和 P₃ 出现的次数都比 C₄ 少。 K₁ 显然出现了 12 次。 P₂ 显然出现了 6 × 6 = 36 次。任意选择左边的 2 个顶点和右边的 1 个顶点，或者任意选择左边的 1 个顶点和右边的 2 个顶点，都能得到诱导子图 P₃ ，因而它一共出现了 C(6, 2) × 6 + 6 × C(6, 2) = 180 次。最后，任意选择左边的 2 个顶点和右边的 2 个顶点，都能得到诱导子图 C₄ ，因而它一共出现了 C(6, 2) × C(6, 2) = 225 次。