2008-08-16 0:40| 
10 Comments | 本文内容遵从 
线段AC上有一点B。以AB和BC为边，分别构造等边三角形XAB和YBC。证明，以下七个点共圆：点B，XC和YA的交点，以及线段AC、XC、YA、XB、YB的中点。
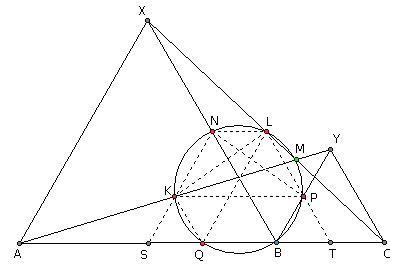
如图，S为AB的中点，T为BC的中点。首先注意到，△ABY和△XBC全等(SAS)，也就是说△XBC是△ABY绕B点旋转60°得到的，因此AY和XC的夹角∠AMX=60°。注意到中位线LQ∥AX，中位线KQ∥CY，我们立即得到∠KQL也等于60°，于是K、L、M、Q四点共圆。
另外，中位线NL∥BC，中位线KP∥AB，因此线段NL、KP和AC全都平行。又中位线PT∥YC，YC∥XB，而XB与中位线LT平行，因此PT∥LT，即P、L、T三点共线。于是我们得知∠LPK=∠LTB=60°。类似地，∠NKP也等于60°，因此四边形KNLP是一个等腰梯形，这四个点共圆。而∠LPK也是弦KL所对的圆周角，因此这个圆和前面的那个圆是同一个圆，L、N、K、Q、P、M都在这个圆上。又∠NBP=60°=∠NKP，它们都是NP所对的圆周角，因此B也在这个圆上。
来源：http://www.cut-the-knot.org/Curriculum/Geometry/TwoEquilateralBumps.shtml
a sofa
先占个座位
翻译得不错 似乎那个网站很棒啊 看原文更有感觉 呵呵
看见SAS总是让我想起初中时无穷无尽的几何证明题
不错，感觉上这个很有意思。
我记得……狗狗给我说过个类似的……
=.=好像叫做九点共圆吧……
九点共圆~~诡异的东东~~MS和三角形滴几条线有关~
还有个“五点共圆”：
http://www.cyol.com/zqb/content/2001-04/06/content_200107.htm
《中国青年报》有个“五点共圆”问题：
http://www.cyol.com/zqb/content/2001-04/06/content_200107.htm
中国青年报 China Youth Daily 2001年4月6日 星期五
为什么网址贴不上来：
h t t p : / / w w w . c y o l . c o m / z q b / c o n t e n t / 2 0 0 1 - 0 4 / 0 6 / c o n t e n t _ 2 0 0 1 0 7 . h t m
看了那么多字母就晕了……
虽然能看懂……