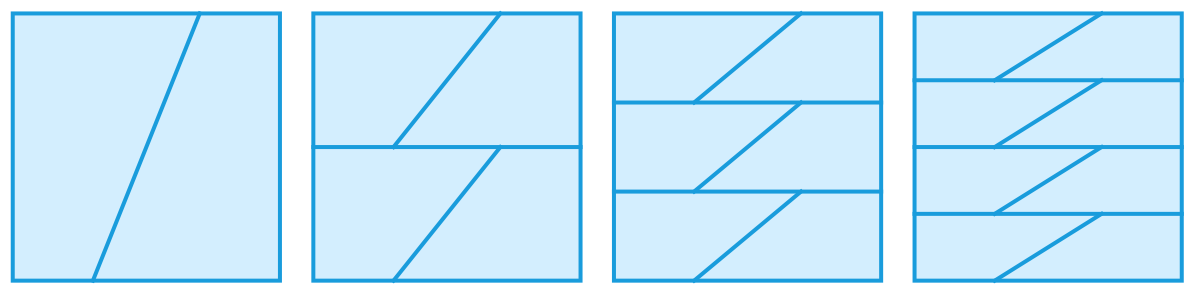
1969 年, David Klarner 提出了这样一个问题:能否把一个长方形划分成奇数个全等的小块,并且这些小块不能是小长方形?如果把问题改为偶数个小块,这件事情是很容易做到的,如下图所示。对于奇数个小块的情况,问题显然就没有那么简单了。继续阅读下去之前,你不妨先想一想。
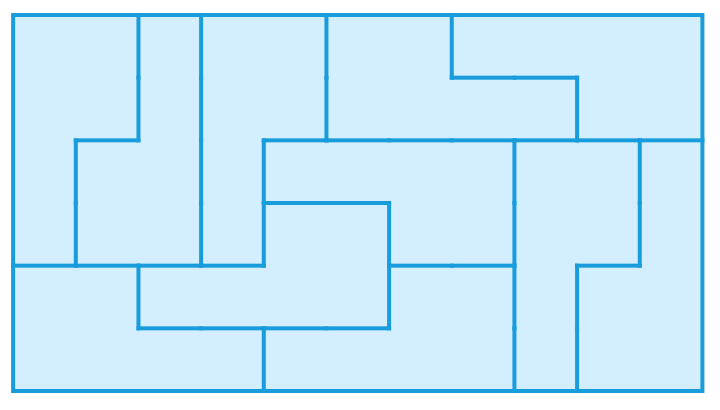
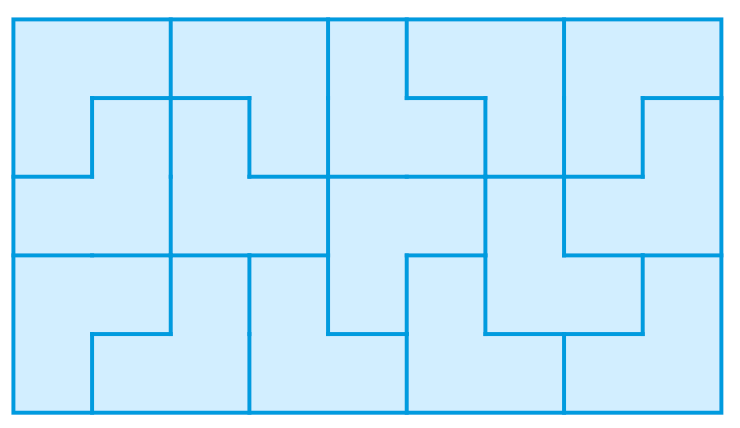
答案是肯定的。 David Klarner 自己给出了两个这样的例子:
我是在 Unsolved Problems in Geometry 一书里看到这个问题的。
1969 年, David Klarner 提出了这样一个问题:能否把一个长方形划分成奇数个全等的小块,并且这些小块不能是小长方形?如果把问题改为偶数个小块,这件事情是很容易做到的,如下图所示。对于奇数个小块的情况,问题显然就没有那么简单了。继续阅读下去之前,你不妨先想一想。

答案是肯定的。 David Klarner 自己给出了两个这样的例子:


我是在 Unsolved Problems in Geometry 一书里看到这个问题的。