若干个顶点以及某些顶点和顶点之间的连线，就构成了一个“图”。如果对某个图进行变换，使得原来任意两个有连线的顶点之间都不再有连线，原来任意两个没有连线的顶点之间现在都有连线了，那么所得到的图就是原来那个图的“补图”。如果一个图和它的补图具有本质上完全相同的结构（这意味着，把其中一个图的顶点以适当的方式与另一个图的顶点建立一一对应的关系，那么对于谁和谁之间有连线、谁和谁之间没有连线这样的问题，两个图的情况是完全一样的），我们就说这个图和它自己是互补的。下图显示了一个顶点数为 5 的图以及它的补图，容易看出，它们的本质结构是相同的。这说明，顶点数为 5 的图有可能和自己互补。
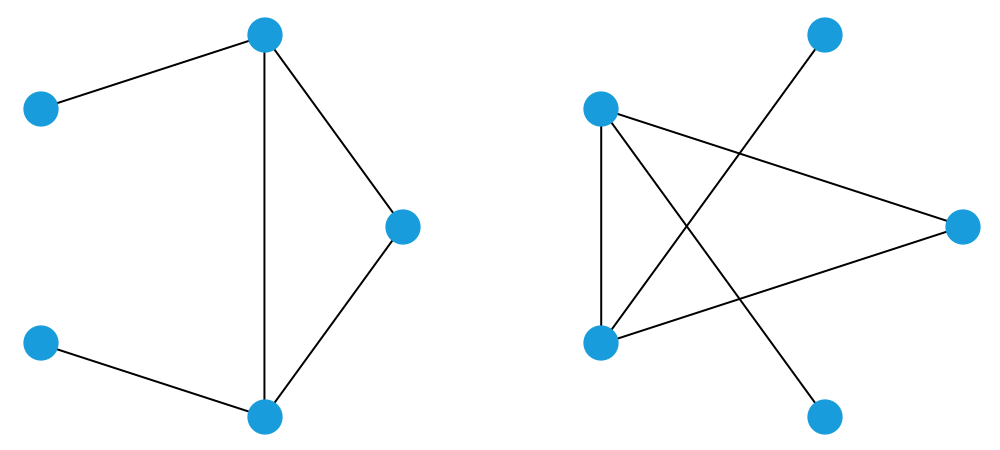
下图显示了一个顶点数为 8 的图，它和它的补图也具有同样的本质结构（你能看出来吗）。这说明，顶点数为 8 的图也有可能和自己互补。
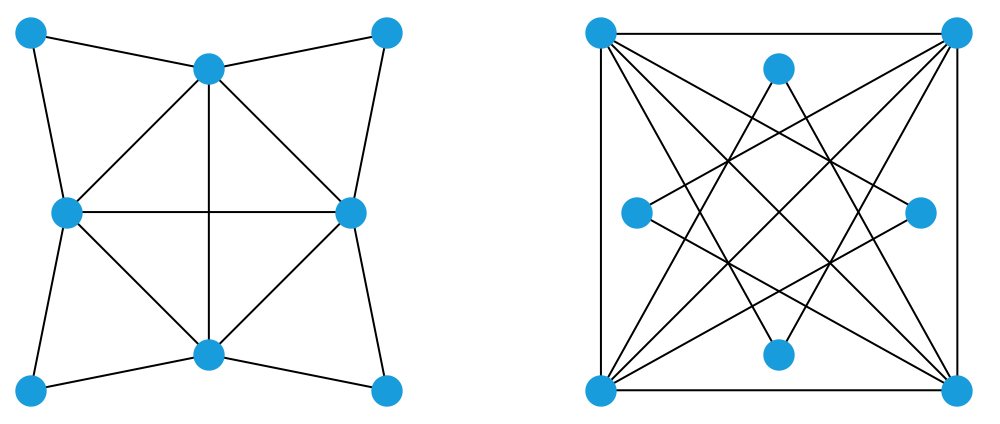
我们今天的问题是：对于那些正整数 n ，存在顶点数为 n 的与自己互补的图？
如果一个图有 n 个顶点，那么它总共就有 n(n-1) / 2 条可能的连线。显然，一个图要想和自己互补，它里面的连线数必然是 n(n-1) / 2 的一半，因此 n(n-1) / 2 必须得是偶数。这说明， n 只能等于 1, 4, 5, 8, 9, 12, 13, 16, 17, … ，即那些形如 4k 和 4k + 1 的数。
接下来，我们将会构造性地说明，对于上述的每一个 n ，顶点数为 n 的图都确实有可能和自己互补。当 n = 1 时，整个图只有 1 个顶点，没有任何连线，根据定义，它和它自己是互补的。当 n = 4 时，一条简单的“链”便满足要求：不妨把这 4 个顶点分别记作 x 、 y 、 z 、 w ，那么 x – y – z – w 的补图就是 y – w – x – z ，整个图的本质结构并未发生改变。
另外，对于任意一个有 k 个顶点的且与自己互补的图，在它外面添加一根由 4 个新顶点组成的链条 x – y – z – w ，再把顶点 x 与所有 k 个顶点都相连，把 w 也与所有 k 个顶点都相连。容易看出，整个图现在就有 k + 4 个顶点了，并且这个新的图也和自己是互补的。
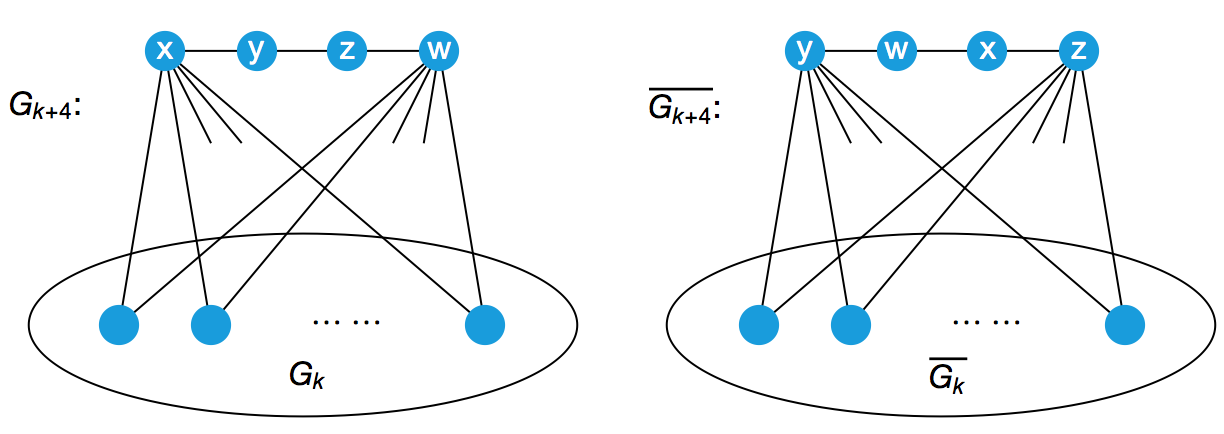
因此，我们就可以从 n = 1 和 n = 4 的情形出发，借助上面的扩展方法，依次得到 n = 5, n = 8, n = 9, n = 12, … 的构造。这立即说明，对于所有形如 4k 和 4k + 1 的正整数 n ，顶点数为 n 的图都确实有可能和自己互补。
问题及解答出自 2000 年 Stephan C. Carlson 在 Mathematics Magazine 的一篇文章。我是在 Proofs Without Words 2: More Exercises in Visual Thinking 一书中看到这个问题的。
已阅。
已阅。
阅
大家开始疯狂发“阅”了。。。。
这道题在图论导引的课后习题里也有一个构造证明，它是把4k分为4个k，每个分别是x y z w，然后按顺序连过来，令x和w为图H，y和z为H补，然后整个图就自补了，4k+1的证法就是让多的那个点连到x和w的每一个点上，整体证明看起来好像不太一样，但我觉得内核思想还是一样的，对吧？
其实只要把图展开成具有互不相交的边的图的形式，再比较，很容易看出是否自互补
大哥，你的博客文章好难浏览啊，没有说目录能一目了然看一列吗？
Trivial……构造全同的图而已……
我之前在想一个有向图全同性判定的问题……发现貌似没有什么很好的办法。
请问什么是全同？
@楼上，就如上文说的，“把其中一个图的顶点以适当的方式与另一个图的顶点建立一一对应的关系，那么对于谁和谁之间有连线、谁和谁之间没有连线这样的问题，两个图的情况是完全一样的”，只不过对于有向图，还要加上连线的方向也是完全一样的。
你以尝试搜索下 图同构 或者 Graph Isomorphism, 对于此 NP 问题目前也有不少相对还算有效的算法了.
想问一下2个顶点或者3个顶点的他们怎么不能跟自己互补了？看不懂互补的性质，谢谢！
2个顶点构成的“图”，就只有连线或者不连线两种情况，但是这两种情况互补，而不是每种情况和自己互补，所以不行。而三个点，只有三条可能存在的连线。一共存在0123条线4种情况，其中13互补，12互补，没有自己和自己互补的情况。
其实4k，4K＋1那段分析已经很到位了，这篇文章也没什么阅读难点啊。
挺有意思的问题。
我理解，4k以及4k＋1本质上就是1和4的组合。可以简化理解为，一切自己互补的图，都是按照1和4两种模式迭代衍生出来的。
投资知识是明智的，投资网络中的知识就更加明智。