我们很容易在平面内放置很多点，使得任意两点确定的直线都只经过这两个点——你需要做的，仅仅是让任意三点都不共线就行了。那么，能否在平面内放置若干个点，使得任意两点确定的直线总是恰好经过三个点呢？更一般地，对于任意正整数 n > 2 ，能否在平面内放置若干个点，使得任意两点确定的直线总是恰好经过 n 个点呢？当然，我们要排除掉所有点都共线这种平凡的情况。

记得我很小的时候就想过这个问题。小时候有一种经典的智力题，大致就是叫你把多少多少棵树种成多少多少行，使得每行都有多少多少棵树。比方说，如何把 9 棵树种成 10 行，使得每行都有 3 棵树？答案如下图所示。但请注意，其实图中还有不少直线上只有 2 棵树，比如那条蓝色的虚线。

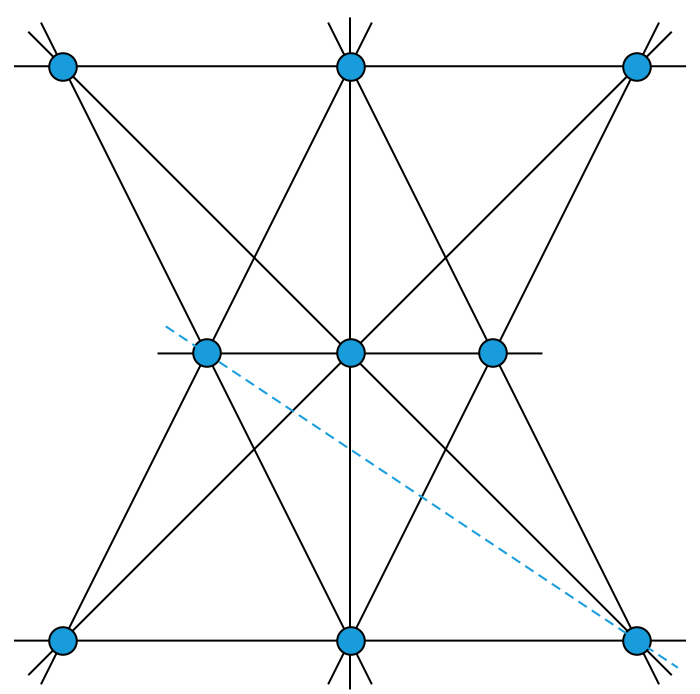
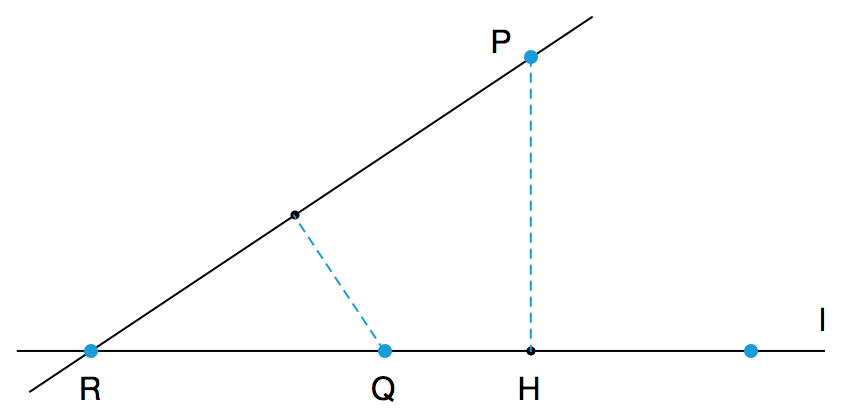
当时，我就曾经想过，如果树苗足够多，能否让每条可能的直线上都种有 3 棵树呢？于是，我没事儿就来尝试一番，但每一次都以失败告终。后来我才知道，这是不可能的。根据 Sylvester–Gallai 定理，在任意一个有限点集中，一定有一条直线恰好只经过两个点，除非所有的点都是共线的。这个定理有一个非常漂亮的证明，这里不得不提。假设存在某个点集，满足任意两点确定的直线上都存在其他的点。画出所有可能的直线，作出每一个点到每一条直线的垂线段，然后找出所有这些垂线段中最短的一条。不妨假设这条最短的垂线段是点 P 到某条直线 l 的垂线段，垂足点记作 H 。由假设， l 上至少有三个点，因此至少有两个点分布在垂足 H 的同一侧（允许和垂足重合）。不妨把这两个点记作 R 、 Q ，如下图所示。由于我们画出了所有可能的直线，因此 P 、 R 两点之间也有一条直线；此时， Q 到 PR 的垂线段就是更短的垂线段，于是产生矛盾。要想避免这样的矛盾，唯一的方法就是，所有的垂线段长度都为 0 ，换句话说我们根本作不出所谓的垂线段。这也就是所有点全都共线的情况。

我们刚才证明了，在一个点集中，只经过两点的直线一定存在，除非所有点全都共线；因此，当 n > 2 时，我们自然就无法让每条可能的直线上都有 n 个点，除非所有点全都共线。

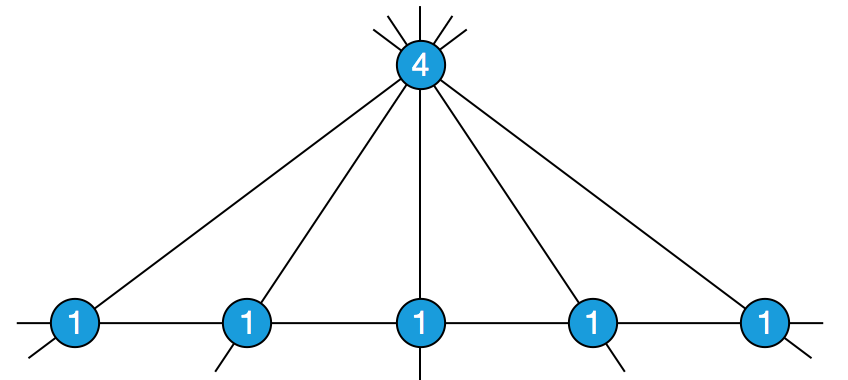
1971 年，U. S. R. Murty 提出了这么一个问题：如果允许有重合的点，那么刚才的问题有解吗？答案是肯定的。如下图，每个写有数字 1 的圆盘表示一个点，那个写有数字 4 的圆盘则表示一个四重点。你会发现，每条可能的直线上都经过了恰好 5 个点。类似地，把 n 个点摆成一条直线，再在直线外放置一个 n – 1 重点，那么每条可能的直线都会经过恰好 n 个点。另外，对于一个合法的解来说，如果把每个点的重数都扩大到原来的 k 倍，所得图形自然也满足要求；但我们认为，它和原图形是本质上相同的解。

我们今天的问题就是： Murty 的问题还有什么本质上不同的解吗？

 

 

 

 

 

 

 

 

答案仍然是肯定的，如下图所示。容易看出，每条可能的直线上都有恰好 4 个点。利用刚才提到的翻倍法修改每个点的重数，还会得到又一批本质相同的解。

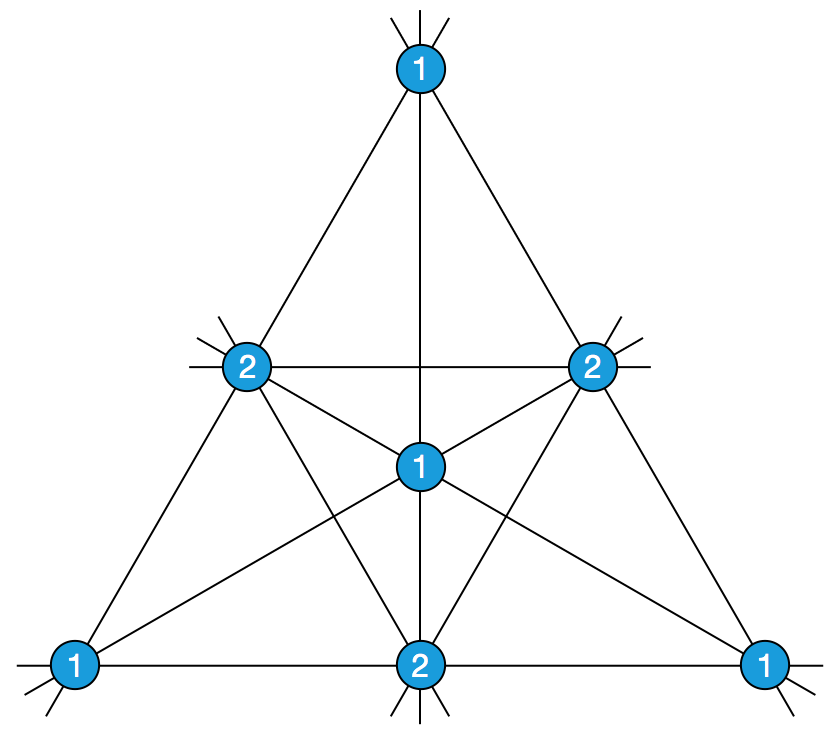
有趣的是， Murty 再也找不到其他的解了。他猜测，这个问题确实没有别的答案了。换句话说， Murty 认为，如果平面内有若干个点，每个点都有一个权重，且任意两点确定的直线所经过的点的权重之和都相等，则可能的情况只有以下四种：

1. 点集中的任意三点都不共线；
2. 所有点都在一条直线上；
3. 除一点外，其余所有点都在一条直线上；
4. 上图所示的情况。

2007 年， Eyal Ackerman 、 Kevin Buchin 、 Christian Knauer 、 Rom Pinchasi 和 Günter Rote 证明了， Murty 的猜想是正确的。你可以在这里看到他们的论文。