如果让你设计一种用于人工智能测试的谜题，你会怎么设计？俄国计算机科学家 Mikhail Moiseevich Bongard 在 1967 年出版的 Проблема Узнавания 一书中提出了一种“图形分类依据”型的谜题。谜题的规则很简单：现已按照某种依据把 12 张图片分成了左右两组（每组各 6 张），问依据是什么。在 Проблема Узнавания 的附录中， Bongard 自己出了 100 道题，并把它们依次编号为 1, 2, 3, …, 100 。很多题目对于人类来说非常简单，分类依据几乎是一目了然；但是，要想设计某种算法让计算机自动解出，则是一件看上去几乎不可能完成的任务。下面这张图是书上第 283 页的三个谜题。第 7 号谜题的答案是，左边的图形都是竖着的，右边的图形都是横着的；第 8 号谜题的答案是，左边的图形都在右边，右边的图形都在左边；第 9 号谜题的答案是，左边的图形都是平滑的线条，右边的图形都是波浪形线条。
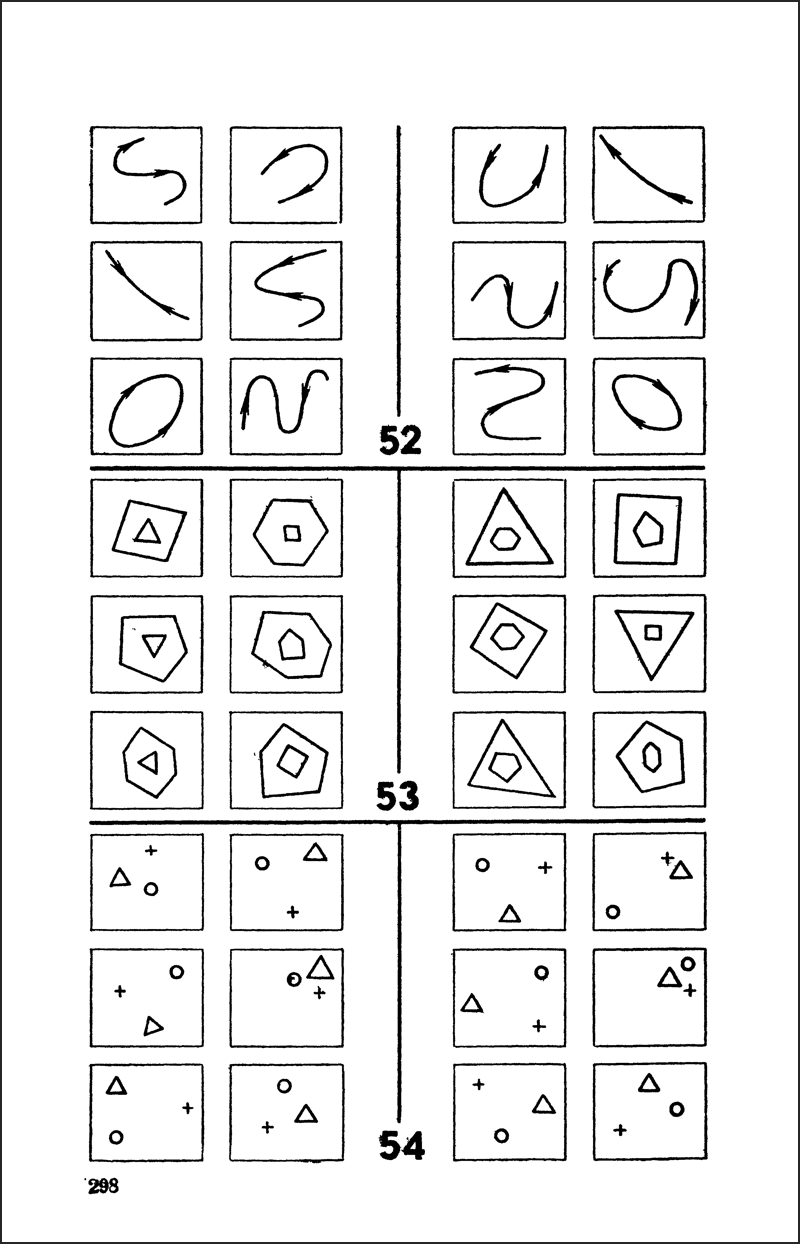
这 100 道题里还有很多难题，可能是人类也要看半天才能看出来的。下面这张图是书上第 298 页的三个谜题。第 52 号谜题的答案是，左边的图形箭头方向相反，右边的图形箭头方向相同；第 53 号谜题的答案是，左边的图形中外面那个多边形拥有更多的边，右边的图形中里面那个多边形拥有更多的边；第 54 号谜题的答案是，左边的图形顺时针依次是＋○△，右边的图形逆时针依次是＋○△。
1970 年，这本书的英译版 Pattern Recognition 登陆美国。认知科学专家 Douglas Hofstadter 对附录中的这些谜题产生了极大的兴趣。他把这些问题叫做 Bongard 问题，并且还自编了 56 道新的问题。在他的神作 Gödel, Escher, Bach: An Eternal Golden Braid 一书中， Bongard 问题也没少出镜。
Harry Foundalis 对 Bongard 问题也非常感兴趣。他在已有题库的基础上又增加了 44 道题目，从而把问题的编号扩展到了 200 。你可以在 Foundalis 的个人网站上看到这些谜题。
最近，我也迷上了 Bongard 问题。我从这 200 道题目中选择了 45 道题，并把它们分成了简单、中等、困难三个难度，每个难度各 15 道题。很多简单题都会让我产生一种超越机器的自豪感，同时也会让我由衷地敬佩题目作者变着法子虐人工智能的能力。个别难题则真的非常非常难，足够荒废大家一下午的时间了。希望大家能够喜欢。
EASY 01.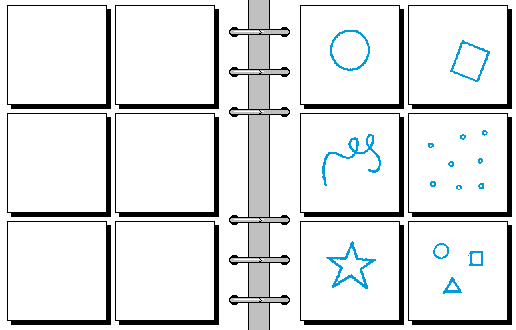 
EASY 02.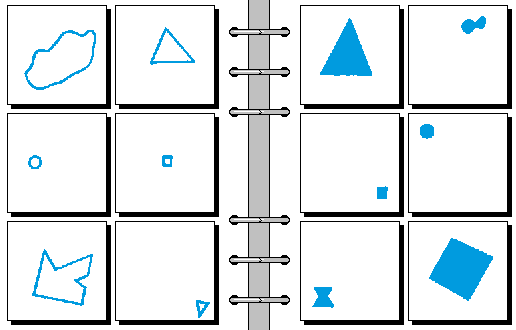 
EASY 03.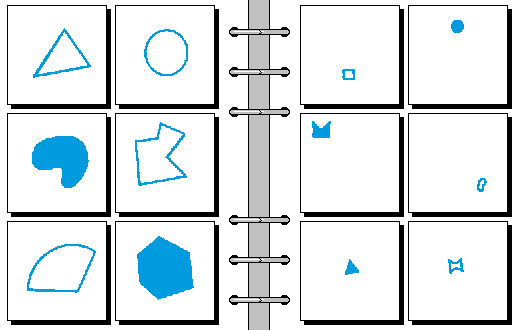 
EASY 04.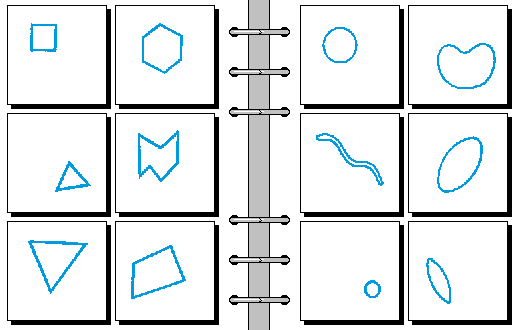 
EASY 05.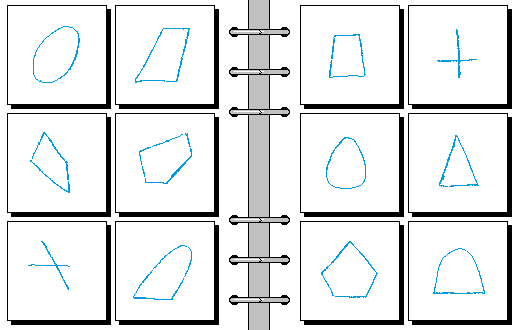 
EASY 06.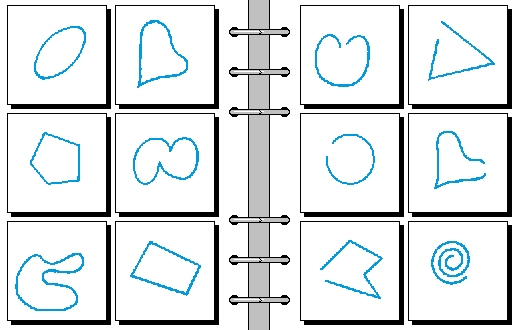 
EASY 07.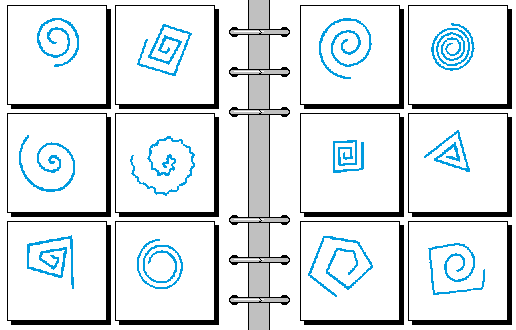 
EASY 08.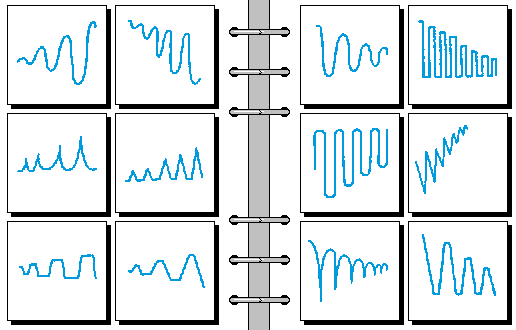 
EASY 09.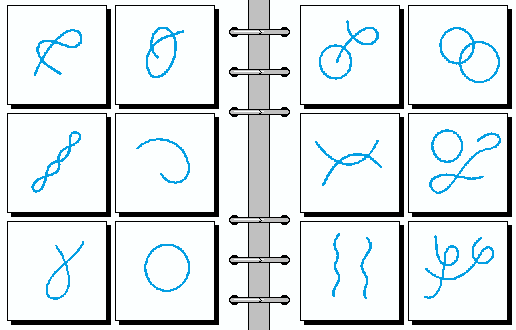 
EASY 10.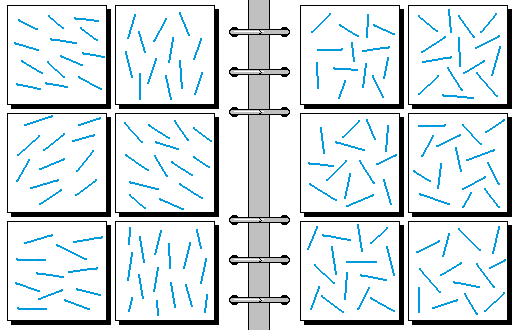 
EASY 11.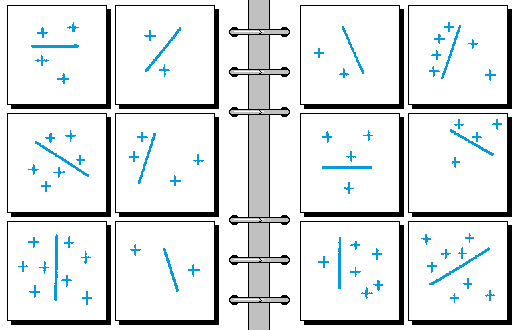 
EASY 12.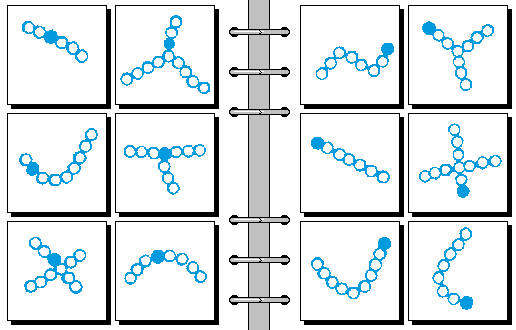 
EASY 13.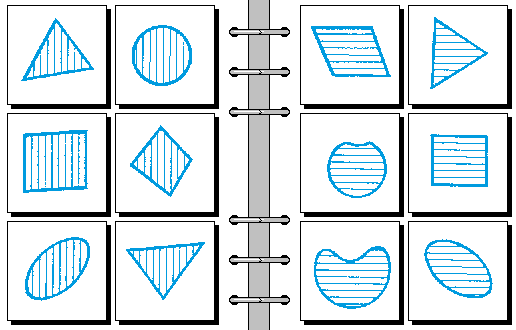 
EASY 14.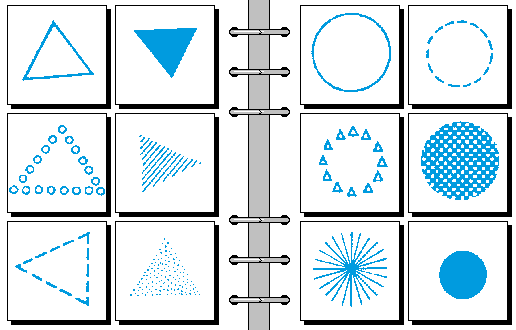 
EASY 15.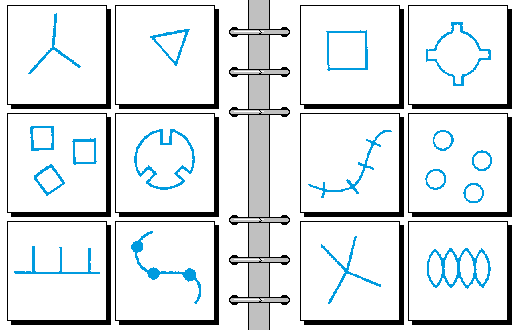 
答案：
- 无 | 有
- 空 | 实
- 大 | 小
- 直边 | 曲边
- 歪斜 | 对称
- 封闭 | 有缺口
- 顺时针 | 逆时针
- 渐强 | 渐弱
- 一条线 | 两条线
- 方向统一 | 方向杂乱
- 两侧数量相等 | 两侧数量不等
- 实心圆在内部 | 实心圆在端点
- 竖纹 | 横纹
- 三角形 | 圆形
- 三 | 四
MEDIUM 01.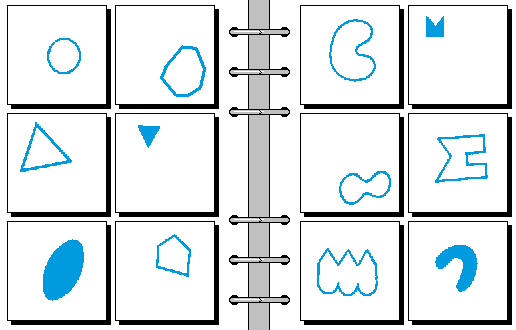 
MEDIUM 02.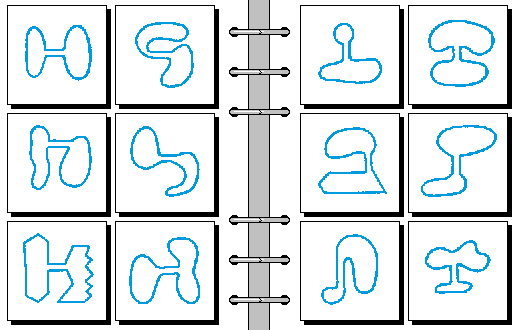 
MEDIUM 03.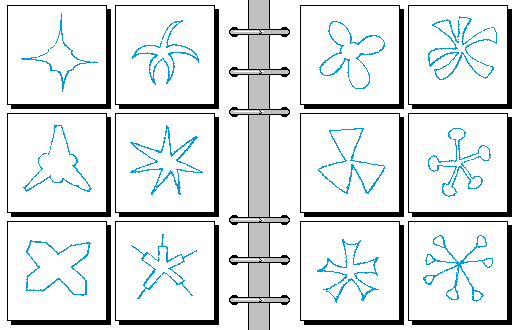 
MEDIUM 04.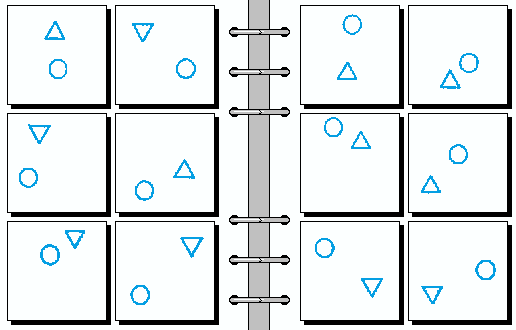 
MEDIUM 05.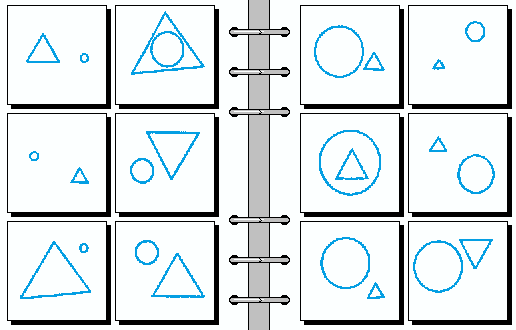 
MEDIUM 06.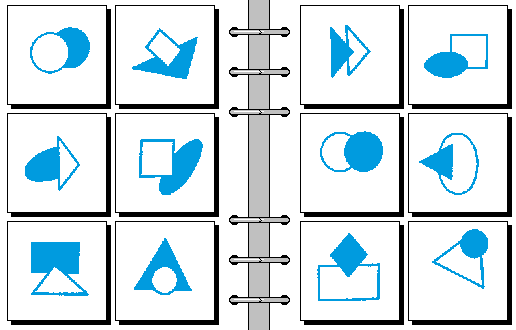 
MEDIUM 07.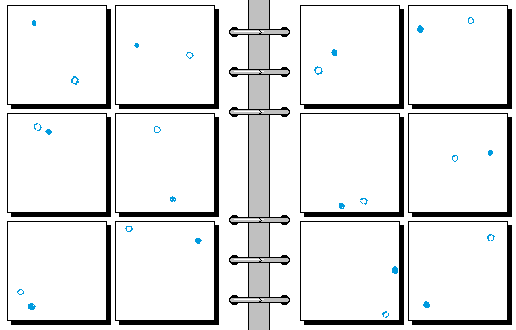 
MEDIUM 08.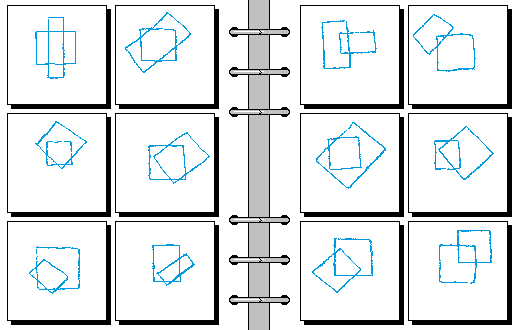 
MEDIUM 09.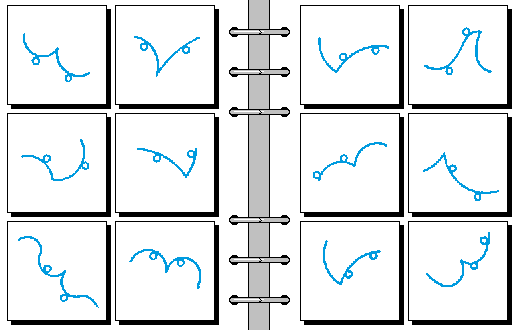 
MEDIUM 10.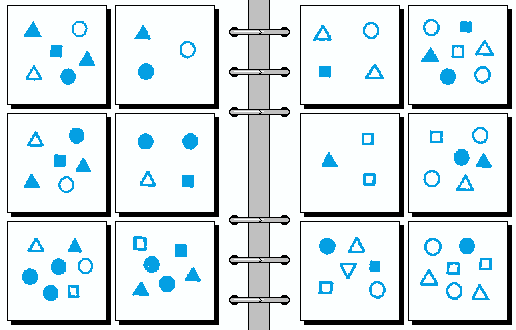 
MEDIUM 11.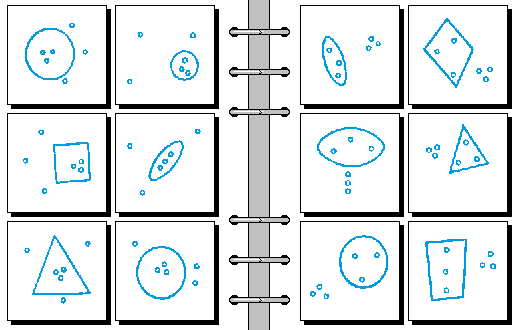 
MEDIUM 12.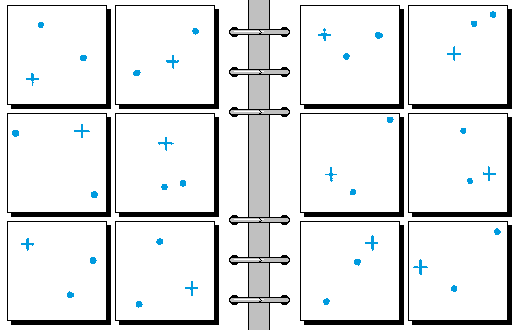 
MEDIUM 13.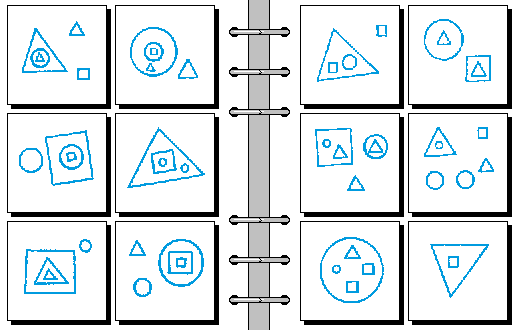 
MEDIUM 14.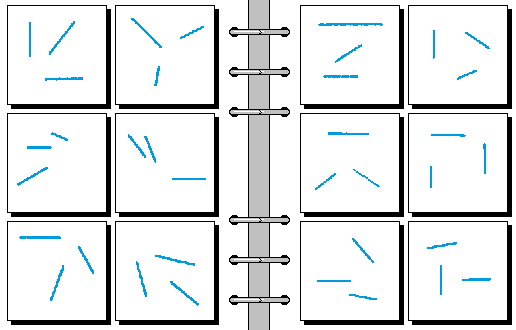 
MEDIUM 15.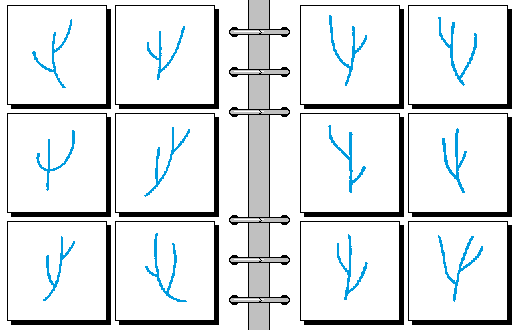 
答案：
- 凸图形 | 凹图形
- 水平通道 | 竖直通道
- 末梢逐渐变小 | 末梢逐渐变大
- 三角形在圆形上 | 三角形在圆形下
- 三角形比圆大 | 三角形比圆小
- 空心图形覆盖实心图形 | 实心图形覆盖空心图形
- 两点连线成 \ 形 | 两点连线成 / 形
- 四个交点 | 两个交点
- 圆圈在不同分支上 | 圆圈在同一分支上
- 实心物体更多 | 空心物体更多
- 框内的三个圆圈距离很近 | 框外的三个圆圈距离很近
- 加号到两个圆点距离相等 | 加号到两个圆点距离不等
- 图形嵌套可达两层 | 图形嵌套最多一层
- 三线延长后交于一点 | 三线延长后不交于一点
- 左分支的顶端比右分支低 | 左分支的顶端比右分支高
HARD 01.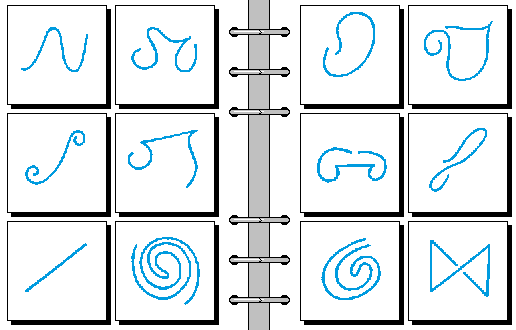 
HARD 02.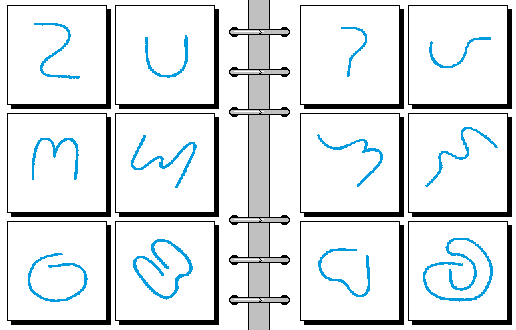 
HARD 03.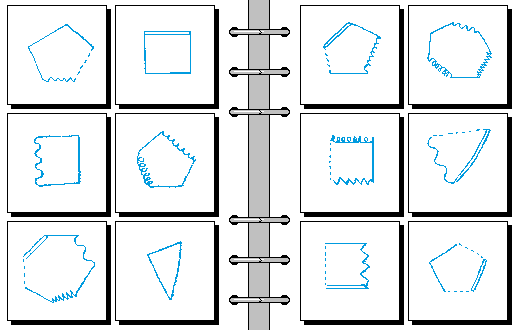 
HARD 04.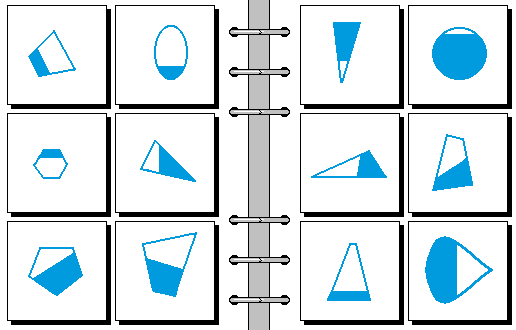 
HARD 05. 
HARD 06.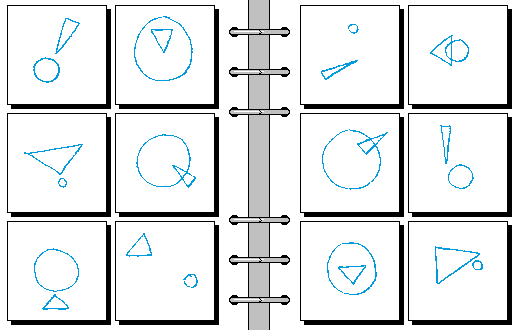 
HARD 07.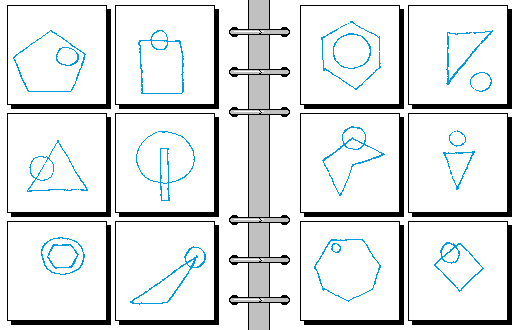 
HARD 08.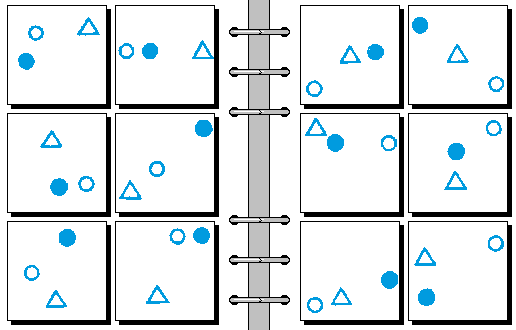 
HARD 09.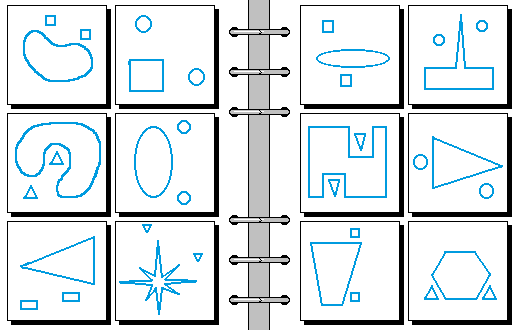 
HARD 10.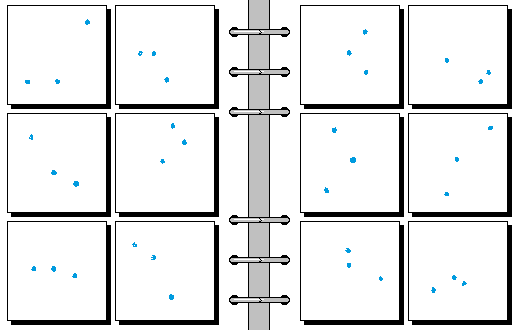 
HARD 11.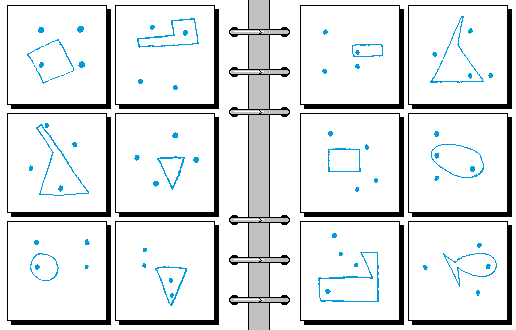 
HARD 12.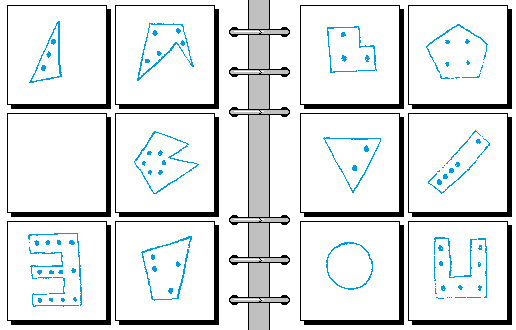 
HARD 13.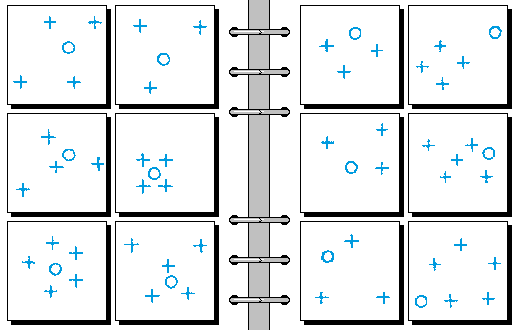 
HARD 14.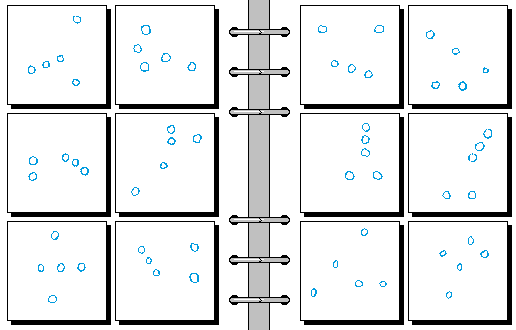 
HARD 15.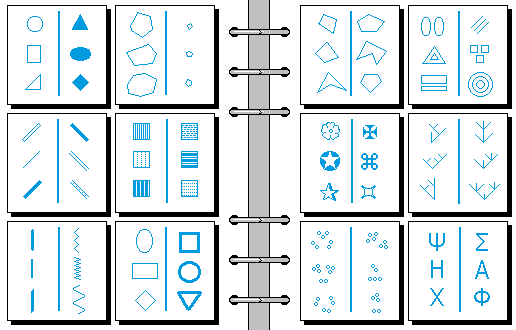 
答案：
- 线条两端距离很远 | 线条两端距离很近
- 线条首段和尾段平行 | 线条首段和尾段垂直
- 有三条简单型的边 | 有三条修饰型的边
- 实心部分正往宽处漫延 | 实心部分正往窄处漫延
- 连接后成等腰三角形 | 连接后成斜三角形
- 三角形指向圆心 | 三角形不指向圆心
- 多边形以某条边为底 | 多边形以某个顶点为底
- 实心圆离空心圆更近 | 实心圆离三角形更近
- 两个小物体之间的连线不被阻挡 | 两个小物体之间的连线会被阻挡
- 三个点的横坐标等距 | 三个点的纵坐标等距
- 四个点构成平行四边形 | 四个点不构成平行四边形
- 边数和点数相等 | 边数和点数不等
- 圆圈在加号构成的凸包内 | 圆圈在加号构成的凸包外
- 去掉共线三点后剩下两点呈 : 状 | 去掉共线三点后剩下两点呈 · · 状
- 依据性质进行分类 | 依据数量进行分类
已阅。
是不是花了一下午时间？
研究研究
easy6不如用每个连通块凸包面积判断吧。右边最后一个图线条并不短
medium10我看的是是否有空心物体重复两次，似乎搞复杂了
hard10没看出来
后面和横竖方向有关的都略坑
EASY 06 确实不太好，而且与之前分大小的那道题略有重复。我把这道题换了（并且调整了一下顺序）。
medium11 我的看法是右边的框框的大小足够框起来在外面的3个小圈
左边的框框不够大 :P
Hard部分的题目真的很难想到
继续支持发blog ^_^
弱弱问下51答案是啥，就是全文第三幅图 http://www.foundalis.com/res/bps/bongard/p051.htm
可能是 左：至少有两个点距离<x； 右：不存在距离<x的一对点
左边两点相连等距两条直线，右边不等距
HARD 15
左边的容易右边的难…算不算？
水一发
我能说我大部分Easy都不会做吗？
我也来出一组：八，人，入；且，旦，目
对AI来说困难的题目，都是：一个人类可以十分简单地做出正确的判断，但当你问他通过怎样的思考方式才做出的这个判断，他却答不上来的。这样的题目，人类无法为AI设计解题算法。
答案都写得这么清楚了，人只要穷举或者用接近穷举的方法即可。
答不上来只是因为解释出来太长。就像程序把整个计算过程列出来也很长，人也一样很难理解。
而程序本身，因为只是一个穷举程序，人看了也不会信服……
@wavebat 人类只是在大脑中内置了几种模式匹配的变换算法而已。你问他通过怎样的思考方式，他当然答不上来他动用了哪种内置算法呀。
这些内置算法的数量有限，组合也有限。这些内置算法大都可以通过人工神经网络、编程实现。
所以这些题，对AI困难只是因为没有预先输入知识，让AI预先学到这些分类方式而已。
AI没有预先输入知识就无法答出这些题(但人类可以)是不是说明AI仍不能通过测试？
这些问题大都可以通过人工神经网络预先训练、外加编程手段实现的变换规则让AI能答对。
又看了一下，Hard组的问题基本上都需要逻辑推理，所以不但需要机器推理，还需要大量背景知识。目前的人工智能水平应该解不出。
67，为什么我在MSN里面没有找到你matrix67@tom.com ？？？
已阅读
这种鉴别功能有什么实际应用呢
可以用这种问题作为验证码。
M67，我向你发了封邮件，咨询了一些关于blog的事情，你是不是不用以前那个邮箱了呀？
test
您好，我是一名研究生，最近仔细研究了您的文章《基于大规模语料的新词发现算法》，但是苦于没有人人网的数据集，这种网络新词的识别难度挺大的，就像中国文学一样没有固定的格式，成词标准也不固定，只能说，网络新词用的人多了就成了新词，由于没能找到您的联系方式，固在此打扰您请见谅，希望您能给我一些参考资料。
太棒了太喜欢这种类型的问题了。准备去拜读一下侯大师著作的相关章节。
medium07看不懂，要哭。。
感觉Java想要做成的就是模拟人类的思维，比如说，针对分类的问题的话，属于某一类别的事物把它再次抽象为一个类。
最近看美剧看到了Bongard问题
呆着没事干
hard最后一个我以为是左边的简单右边的难来着= =
哈哈我也是这么以为的！
HARD 07右边第一个图是什么？（滑稽）
正如整数数列有在线百科OEIS来收集一样，Bongard问题也有个在线百科OEBP（https://www.oebp.org/）来收集，如HARD 15在其中编号为BP200。很多Bongard问题的分类依据都超出了单纯的几何图形，你甚至还可以看到包含车/不包含车的reCaptcha图片做成的BP844（…）
Wheen I initialkly commented I seem too hqve
clicked the -Notify me when new comments aare added- checkbox
annd nnow every timne a cmment is added I receive fiur
emals with thee exact samme comment. Is there
a waay you arre abloe too remopve mee froom that service? Thankk you!
cool