5 张矩形的纸片和 6 张圆形的纸片散落在桌面上，如下图所示（其中一张矩形纸片被撕掉了一个角）。考虑所有露在外面的矩形顶点以及纸张边缘处的交点，你能否从中找出四个保证共圆的点？很简单，右下角那个绿色矩形的四个顶点就满足要求，因为矩形的四个顶点显然是共圆的。其实，在这个图里，还有另外三组满足要求的点，你能找到吗？
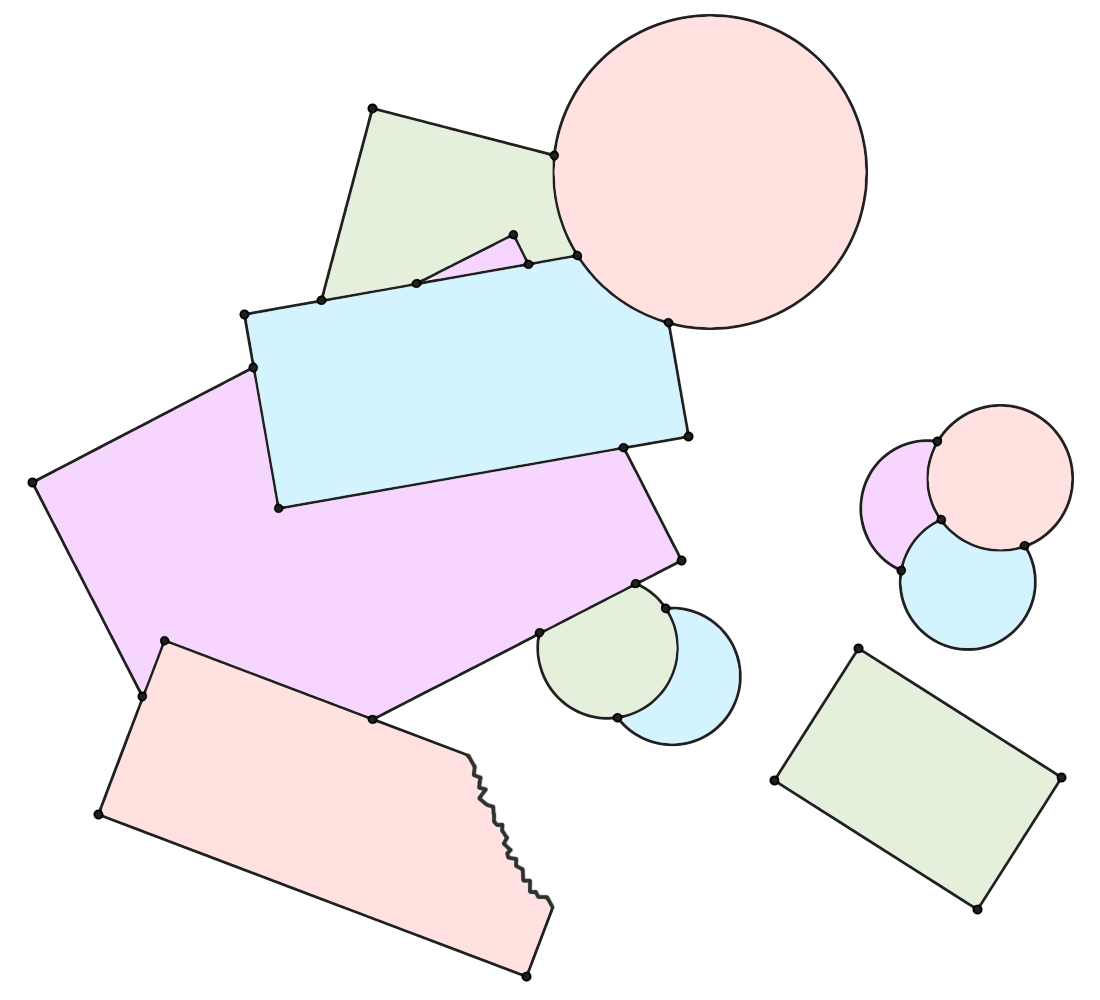
首先， A 、 B 、 C 、 D 这四个点显然是另一组满足要求的点。另一组不太容易找到的点则是 E 、 F 、 G 、 H 这四个点：由于 ∠EFG = ∠EHG = 90° ，因而 E 、 F 、 G 、 H 四点共圆。原题的答案本来到这里就结束了，但有趣的是，题目的原作者自己都没想到，满足要求的点还有一组：由于 ∠EMN = ∠EHN = 90° ，因而 E 、 M 、 H 、 N 四点也是共圆的。
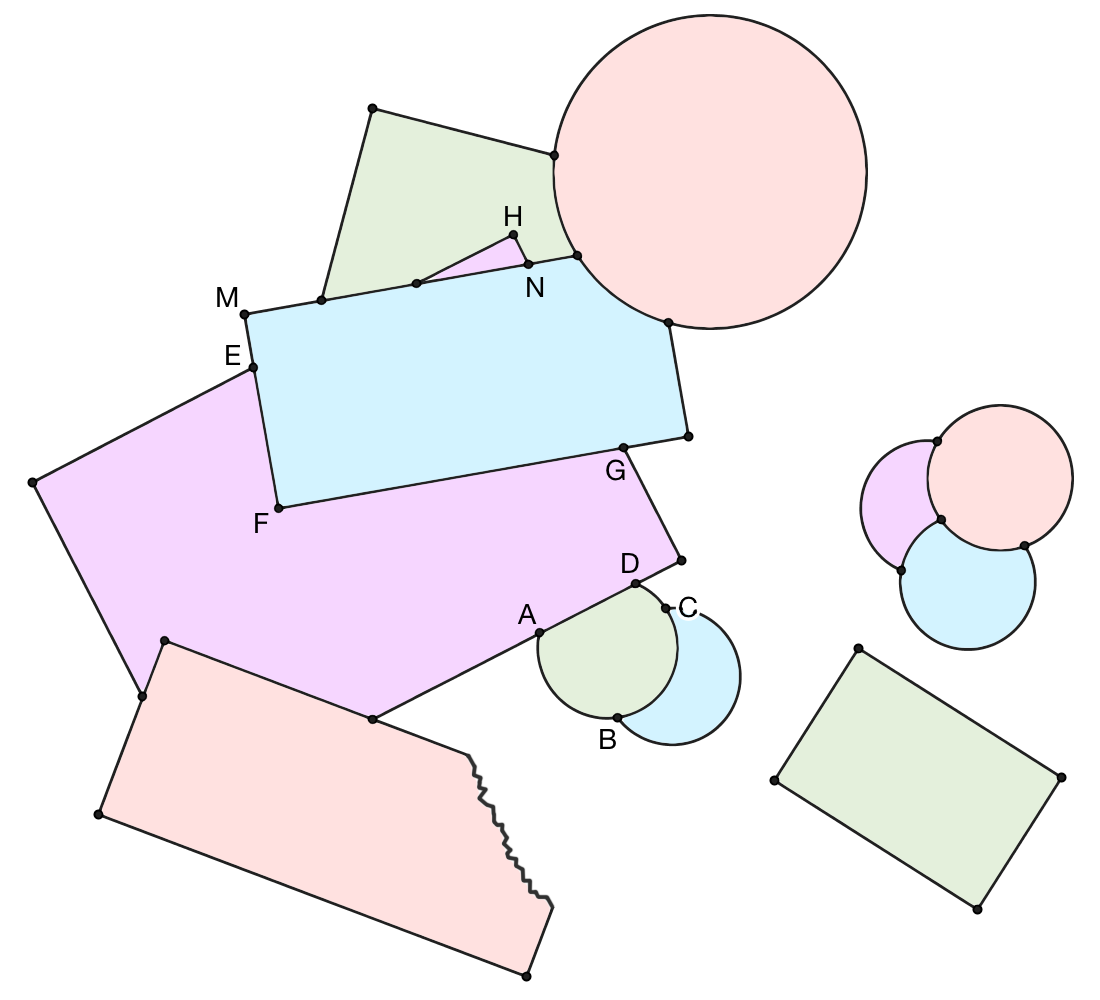
这道题的修改版（用一个额外的圆形纸片盖住了 M 点）收录在了 Stephen Barr 的 Second Miscellany of Puzzles 一书中。我则是在 Martin Gardner 的 The Colossal Book of Short Puzzles and Problems 一书中看到的这道题。
终于来了，慢慢看
伪前排。
Matrix67好长时间不更新了
最后一个是利用折四边形的性质吧
OMG我找了半天只看出來了E 、 M 、 H 、 N 這一組，結果忽略了最明顯的ABCD組。。。
只发现了一组 XD
这题目…似乎偏水啊
终于更新了
板凳
周六下午我花了两三个小时思考这个题。
我很快看出ABCD四点同圆。然后经过初步排查，我排除了那三个相交的圆形，后来又排除了最大的圆、它旁边只露出一角的矩形，以及被撕掉一角的矩形。
我花费了几乎全部时间来找剩下的两组共圆的点。我拿出两本书摆弄各种造型，又排除了一些点的组合，终于发现，有两个直角相交，即EFGH。它们肯定是共圆的，因为我知道圆上以直径为边的三角形都是直角三角形，而有共同斜边的任意个直角三角形都共圆，所以，EFGH共圆。
后来我依据同样的规律试图找出两个相邻的直角三角形，可是没有发现。我几乎放弃，心想最后一组共圆的点肯定很难找出，实在不行就算了吧。可仍不舍得放弃，心想离成功已经很近了，再想想办法吧。于是我开始想，换个角度吧，是否有其他形式的点也能共圆呢？我又将两本书摆弄着，试图以其他角度观察，终于我发现EMHN也是共斜边的两个直角三角形，只不过它们处于直径的同一侧。真是难发现啊！
很开心我坚持出了，并最终自己找出全部三组共圆的点。希望以后能继续如此努力。
very interesting！
右下角那个长方形四个点怎么没有提到
终于有一道可以接受的题目了
这题偏水了。。这就是高中的证明题。