让我们来玩一个游戏。连续抛掷硬币，直到最近三次硬币抛掷结果是“正反反”或者“反反正”。如果是前者，那么我获胜，你需要给我 1 元钱；如果是后者，那么你获胜，我会给你 1 元钱。你愿意跟我玩这样的游戏吗？换句话说，这个游戏是公平的吗？

乍看上去，你似乎没有什么不同意这种玩法的理由，毕竟“正反反”和“反反正”的概率是均等的。连续抛掷三次硬币可以产生 8 种不同的结果，上述两种各占其中的 1/8 。况且，序列“正反反”和“反反正”看上去又是如此对称，获胜概率怎么看怎么一样。

实际情况究竟如何呢？实际情况是，这个游戏并不是公平的——我的获胜概率是你的 3 倍！虽然“正反反”和“反反正”在一串随机硬币正反序列中出现的频率理论上是相同的，但别忘了这两个序列之间有一个竞争的关系，它们要比赛看谁先出现。一旦抛掷硬币产生出了其中一种序列，游戏即宣告结束。这样一来，你就会处于一个非常窘迫的位置：不管什么时候，只要掷出了一个正面，如果你还没赢的话，你就赢不了了——在出现“反反正”之前，我的“正反反”必然会先出现。

事实上，整个游戏的前两次硬币抛掷结果就已经决定了两人最终的命运。只要前两次抛掷结果是“正正”、“正反”、“反正”中的一个，我都必胜无疑，你完全没有翻身的机会；只有前两次掷出的是“反反”的结果，你才会赢得游戏的胜利。因此，我们两人的获胜概率是 3:1 ，我的优势绝不止是一点。

你或许想问，如果已知我的硬币序列是“正反反”，那么你应该选择一个怎样的硬币序列，就能保证获胜概率超过我呢？研究表明，你可以选择“正正反”，这样一来，我们两人的获胜概率将会变为 1:2 ，换句话说你将会有 2/3 的概率获胜。 Using your Head is Permitted 趣题站 2014 年 5 月的趣题对此进行了更深一步的探究。

A 、 B 两人打算玩这么一个游戏。首先， A 选择一个长度为 n 的正反序列，然后 B 再选择另一个长度为 n 的正反序列。之后，不断抛掷硬币，哪名玩家所选的正反序列最先出现，哪名玩家就获胜。我们的问题是，假如两名玩家都采取最优策略的话，对于哪些 n ，游戏对玩家 A 更有利一些（换句话说，玩家 A 拥有超过 50% 的胜率），对于哪些 n ，游戏对玩家 B 更有利一些（换句话说，玩家 B 拥有超过 50% 的胜率）。今后，为了方便起见，我们用数字 1 代表“正面”，用数字 0 代表“反面”。

 

当 n = 1 时，两名玩家的获胜概率显然相同。当 n = 2 时，可以验证，除了 00 打 10 以及 11 打 01 的胜率之比是 1:3 以外，其他所有情况（包括 00 打 11 、 00 打 01 、 01 打 10 、 11 打 10 等四种）的胜率之比都是 1:1 。因而，如果两名玩家都采用最优策略的话， A 一定会选择 01 和 10 之一，从而避免 B 获得 3 倍于自己的胜率。最终结果便是，两人的胜率之比维持在 1:1 的位置，获胜概率仍然相同。令人意想不到的是，当 n > 2 时，游戏总是对玩家 B 更有利的。换句话说，我们要证明，当 n > 2 时，不管 A 选择的 01 串是什么，玩家 B 总能有针对性地选择一个恰当的 01 串，使得他获胜的概率大于 50% 。事实上，我们会证明这样一个结论：玩家 B 总可以截取 A 所选的 01 串的前 n – 1 位，再在前面加上一个数字 0 或者数字 1 作为自己的 01 串，从而使得自己获胜的概率至少有 (2 – (1/2)^n-1)/3 。

不妨把 A 选择的 01 串记作 Py （其中 P 是一个长度为 n – 1 的 01 串， y 则表示数字 0 或者数字 1 ），我们先来看看，如果 B 选择的 01 串是 0P ，结果将会怎样。

不断抛掷硬币，直到最近 n – 1 次硬币抛掷结果正好是序列 P 。这有三种情况：情况一，最近 n 次硬币抛掷结果是 0P ；情况二，最近 n 次硬币抛掷结果是 1P ；情况三，目前硬币抛掷次数还不足 n 次。情况三是最为特殊的，它意味着整个游戏的前 n – 1 次硬币抛掷结果正好就是序列 P ，其概率为 (1/2)^n-1 。让我们假设情况一出现的概率是 p₁ ，则情况二出现的概率就是 1 – (1/2)^n-1 – p₁ 。

如果出现了情况一，那么玩家 B 就直接获胜了，游戏结束；如果出现了情况二或者情况三，那么游戏仍需继续进行下去。不妨把此时的游戏局面叫做节点 X 。现在，玩家 A 离胜利已经非常接近了。如果下一次抛掷硬币的结果正好是 y ，那么玩家 A 就获胜了，游戏结束；如果下一次抛掷硬币的结果是 y （这里 y 表示与 y 相反的数字），那么游戏将会到达另外一个关键的中间状态：最近 n 次硬币抛掷结果为 Py 。对于两名玩家来说，这是全新的起跑线。如果下一次出现 P 的时候，它前面的那个数字是 0 ，那么玩家 B 就直接获胜了，游戏结束；如果下一次出现 P 的时候，它前面的那个数字是 1 ，那么游戏状态又会回到节点 X ，玩家 A 将会再次得到一个制胜的绝佳机会。不妨假设以 Py 打头的随机 01 序列中，下一个 P 的前面正好是数字 0 的概率为 p₂ ，那么下一个 P 的前面正好是数字 1 的概率就是 1 – p₂ 。于是，整个游戏的状态转移图如下图所示。

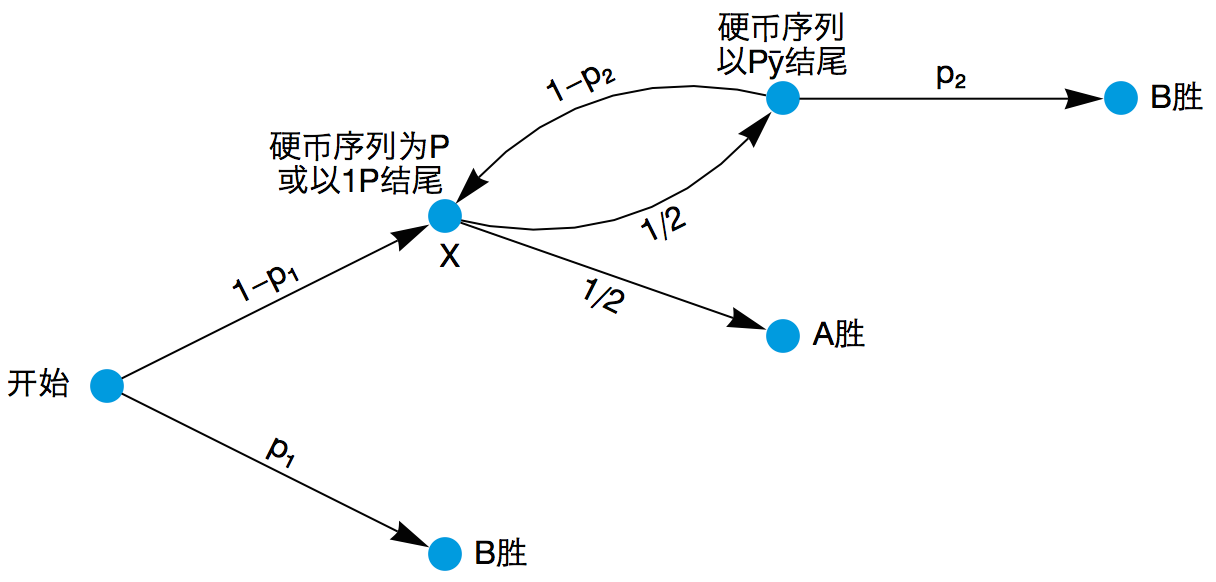
玩家 B 获胜的概率就可以用 p₁ 和 p₂ 表示出来了。首次出现 P 的时候玩家 B 就获胜的概率为 p₁ ，有另外 1 – p₁ 的概率进入节点 X 。进入节点 X 以后， A 将会有 1/2 的概率获胜， B 将会有 (1/2) · p₂ 的概率获胜，其余情况下游戏局面将会回到节点 X ，刚才的各种事件会以相同比例的概率再次发生，并且有可能一遍一遍地重复下去。因此，总的来说，进入节点 X 以后，两名玩家的获胜概率之比是 (1/2) : ((1/2) · p₂) ；进而得出，进入节点 X 以后，玩家 B 获胜的概率就是 ((1/2) · p₂) / (1/2 + (1/2) · p₂) = p₂ / (1 + p₂) 。

综上所述，玩家 B 的获胜概率应为：

W₀ = p₁ + (1 – p₁) · p₂ / (1 + p₂)

别忘了，上述概率值仅仅是 A 在选择了 01 串 Py 之后， B 以 0P 应对时获胜的概率。如果 B 选择以 1P 应对呢？整个游戏的状态转移图将会变成下面这样。

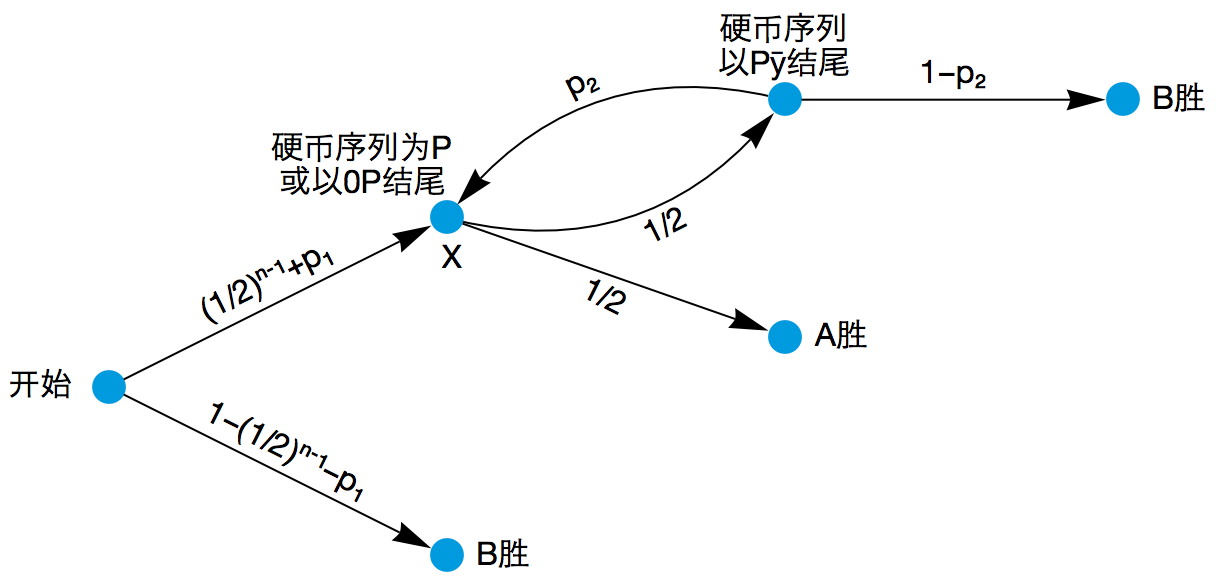
前面我们说过，硬币序列里第一次出现 P 的时候，最近 n 次硬币抛掷结果是 0P ，最近 n 次硬币抛掷结果是 1P ，目前硬币抛掷次数还不足 n 次，这三种情况的发生概率分别为 p₁ 、 1 – (1/2)^n-1 – p₁ 和 (1/2)^n-1 。然而，这次玩家 B 选择的 01 串变成了 1P ，因而游戏开始时进入两条支线的概率就成为了图中所示的那样。另外，从 Py 出发随机产生 01 串，下次出现 P 时它的前面正好是数字 1 的概率为 1 – p₂ ，因而我们需要把第一幅状态转移图当中的所有 p₂ 都替换成 1 – p₂ 。可以计算出，进入节点 X 以后，两人的胜率之比为 (1/2) : ((1/2) · (1 – p₂)) ，其中 B 的获胜概率为

((1/2) · (1 – p₂)) / (1/2 + (1/2) · (1 – p₂)) = (1 – p₂) / (2 – p₂)

玩家 B 的总获胜概率就是：

W₁ = 1 – (1/2)^n-1 – p₁ + ((1/2)^n-1 + p₁) · (1 – p₂) / (2 – p₂)

我们要证明的即是， W₀ 和 W₁ 总有一个大于等于 (2 – (1/2)^n-1)/3 。注意到，如果固定 p₂ 不变，把 W₀ 和 W₁ 都看作是关于 p₁ 的函数，那么 W₀ 将会是一个线性递增函数， W₁ 则是一个线性递减函数，因此最坏的情况将会发生在 W₀ = W₁ 的时候，此时 W₀ 和 W₁ 中的较大值达到最小。解得

p₁ = (1/3) · (2 – (1/2)^n-1 – p₂ – (1/2)^n-1 · p₂)

把上式代回 W₀ 或者 W₁ 当中的任意一个，得到的是一个与 p₂ 无关的数，它正是 (2 – (1/2)^n-1)/3 。下图是 n = 3 时 W₀ 和 W₁ 的图像，可以看到两个图像相交在一起，形成了一条高度大约为 0.58 的交线。至此，我们便成功地证明了，当 n > 2 时，不管 A 选的 01 串是什么， B 总能有针对性地选择另一个 01 串，使得获胜概率可以高达 50% 以上。

 

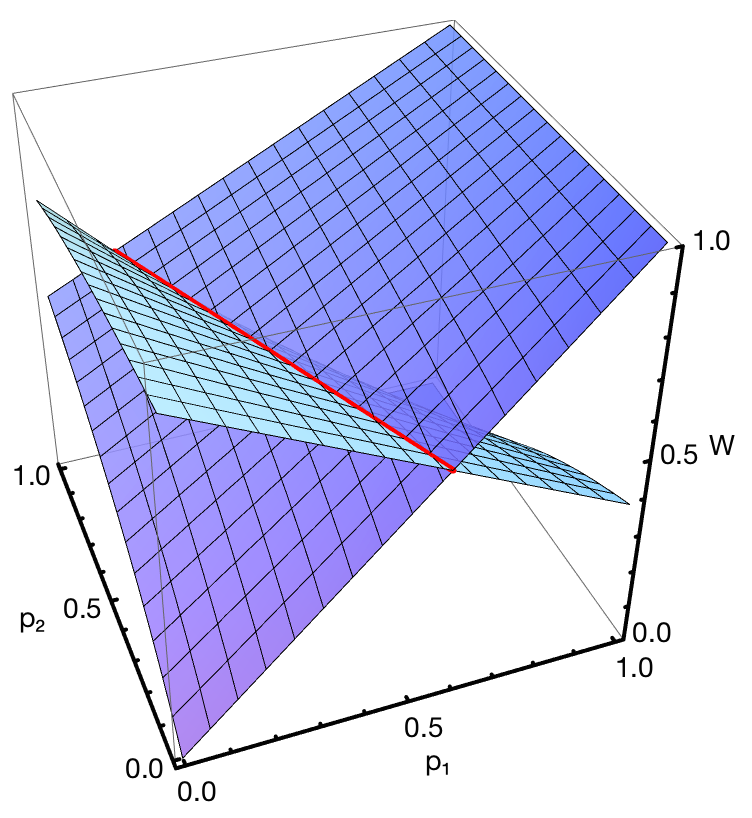
事实上，如果把玩家 A 的选择记作 Py ，那么玩家 B 的最优策略一定就是 0P 和 1P 之一。这个结论是由 Leonidas Guibas 和 Andy Odlyzko 在 1978 年合写的一篇论文里证明的。当 n = 3 时，玩家 B 的最优策略可以归纳如下：

如果 A 选的是	那么 B 应该选	两人的胜率之比
000	100	1:7
001	100	1:3
010	001	1:2
011	001	1:2
100	110	1:2
101	110	1:2
110	011	1:3
111	011	1:7

掌握了上面这个表格的话，你就拥有了一个骗小女生的绝好工具。 YouTube 的 Scam School 系列视频上就介绍了这个 bar trick ：把游戏规则告诉小女生，让她先选一个长度为 3 的硬币序列，然后你再按照上表选择一个对应的硬币序列，你便能保证获得至少 2 倍于她的胜率。重复多次游戏，你将会以很惊人的大比分获胜。你甚至不需要刻意去背表格，只需要记住：如果对方的选择是 wxy ，那么你选择 xwx 就行了。

当然，玩家 B 的最优选择也并不总是把 Py 的第 2 位取反后加在 P 的前面。当 n = 5 时，如果 A 选择了 10110 ，那么 B 选择 11011 会得到 7/12 ≈ 58% 的胜率，而选择 01011 则会得到 17/24 ≈ 71% 的胜率，后者才是他的最优选择。 Leonidas Guibas 和 Andy Odlyzko 认为，玩家 B 究竟是选 0P 更好还是选 1P 更好，这并没有一个明显的规律。

有人或许想问，这些概率值都是怎么计算出来的呀？ John Conway 在 Winning Ways for Your Mathematical Plays 的第 4 卷中提到了一种方法。假如 a 和 b 是两个 n 位 01 串。如果 a 和 b 完全相等，那么记一个数字 1 ，如果不相等，那么记一个数字 0 。接下来，比较 a 的后面 n – 1 位以及 b 的前面 n – 1 位，如果相等，那么接着记一个数字 1 ，如果不相等，那么接着记一个数字 0 。接下来，比较 a 的后 n – 2 位以及 b 的前 n – 2 位，并根据比较结果记下数字 0 或者数字 1 。不断这样做下去，直到最后比较 a 的最后面 1 位和 b 的最前面 1 位，并产生新的数字。在整个过程中，你会依次记下 n 个数字，最终会得到一个 n 位的 01 串。把它当作一个二进制数，并转换成十进制。我们把最终的结果记为 L(a, b) 。举几个例子：

• L(10110, 10110) = (10010)₂ = 18
• L(10110, 01011) = (00001)₂ = 1
• L(01011, 01011) = (10000)₂ = 16
• L(01011, 10110) = (01001)₂ = 9

那么， 01 串 a 和 b 的胜率之比就是

(L(b, b) – L(b, a)) : (L(a, a) – L(a, b))

因此， 10110 和 01011 的胜率之比就是 (16 – 9) : (18 – 1) ，也就是 7:17 。刚才玩家 B 的获胜概率 17/24 ≈ 71% 就是用这种方法算出来的。不过， John Conway 本人似乎从未发表过这个神奇公式的正确性证明。

 

其实，之前在证明这个游戏对 B 更有利的时候，证明过程当中有一个小漏洞，我们有意没说：如果 Py = 000…00 的话，那么 0P 将会等于 Py ；类似地，如果 Py = 111…11 的话，那么 1P 将会等于 Py 。这违反了游戏的规则（两人不能选取相同的 01 串），而且也没法套在刚才的状态转移图里。好在，这两种情况单独分析起来非常容易。事实上，我们很容易证明， A 永远不应该选择 000…00 或者 111…11 ，因为这是最笨的策略。如果 A 选择的是 000…00 ，那么 B 只需要选择 100…00 即可。容易看出，只有开局后的前 n 位硬币序列恰好是 000…00 的情况下， A 才能获胜，如果第 n 次抛掷硬币以后 A 还没获胜的话，那么 B 就锁定胜局了——在出现 000…00 之前， 100…00 必然会先出现。因此， A 的胜率仅为 (1/2)ⁿ ，而 B 的胜率则为 1 – (1/2)ⁿ 。为什么说这是 A 最笨的策略呢？这是因为，不管 A 选择了什么 01 串，他获胜的概率至少也有 (1/2)ⁿ （即开局后的前 n 位硬币序列恰好如 A 所选的情况），因而刚才那种策略的获胜概率已经达到下限，糟糕得不能再糟糕了。类似地，如果 A 选择 111…111 ，那么 B 可以选择 011…11 ，这同样能让 A 的获胜概率降到最低。

讨论到这里，大家肯定想要问：那么， A 的最优策略又是什么呢？

1992 年， János Csirik 在一篇论文中指出，当 n > 3 时， A 的最优策略之一是 1000…0011 （中间有 n – 3 个数字 0 ），此时 B 应该选择 01000…001 来应对，两人的胜率之比将会变成 (2^n-2 + 1) : (2^n-1 + 1) 。当 n = 3 时，查阅上面给出的表格可知， A 的最优策略可以是 010, 011, 100, 101 当中的任意一个。当然， A 的最优策略并不能让 A 的获胜概率大于 50% ，只能让 A 的损失尽可能地小罢了。

 

对了，这个有趣的游戏叫做 Penney’s game ，它是由 Walter Penney 在 1969 年提出来的。