趣题：2014 年 INMO 中的一个问题

这是 2014 年印度全国奥林匹克数学竞赛（INMO）的第 2 题：求证，对于任意正整数 n ，

[n/1] + [n/2] + [n/3] + … + [n/n] + [√n]

总是偶数。这里， [x] 表示不超过 x 的最大整数。

 

 

 

 

 

 

 

 

 

官方给出的解答采用的是数学归纳法。不妨令

f(n) = [n/1] + [n/2] + [n/3] + … + [n/n] + [√n]

容易算出 f(1) = 2 ，这是一个偶数。接下来我们只需要证明，对于所有的正整数 k ， f(k+1) – f(k) 的结果都是一个偶数。注意，如果 i 正好是 k+1 的一个约数，那么 [(k+1)/i] – [k/i] 将会等于 1 ，否则 [(k+1)/i] – [k/i] 都会等于 0 。于是我们有

f(k+1) – f(k) = σ(k+1) + [√k+1] – [√k]

其中 σ(k+1) 表示 k+1 的约数个数。由于一个数的约数总是成对地出现，因而 σ(k+1) 几乎总是一个偶数，除非 k+1 恰好是一个完全平方数；另外， [√k+1] – [√k] 的值几乎总是为 0 ，只有当 k+1 恰好是一个完全平方数时才等于 1 。也就是说，当 k+1 不是完全平方数时， σ(k+1) 是一个偶数，并且 [√k+1] – [√k] = 0 ；当 k+1 正好是完全平方数时， σ(k+1) 是一个奇数，并且 [√k+1] – [√k] = 1 。不管怎样， f(k+1) – f(k) = σ(k+1) + [√k+1] – [√k] 的结果都是一个偶数。至此，结论也就证到了。

有趣的是，当网友在 StackExchange 上提出了这个问题后， David Angell 给出了一个更具启发性的证明。容易看出， [n/1] + [n/2] + [n/3] + … + [n/n] 的值，其实就是第一象限里位于函数 y = n/x 及其下方的整数格点的个数。我们把这些点分成两类：位于一三象限角平分线以外的，以及恰好位于一三象限角平分线上的。前一类的点总是成对地出现，因而一定有偶数个。但是，后一类点并不是成对出现的。那么，这些点一共有多少个呢？注意到，这些点也就是所有形如 (i, i) 的点，其中 i2 不能超过 n 。因而，这样的点一共有 [√n] 个。

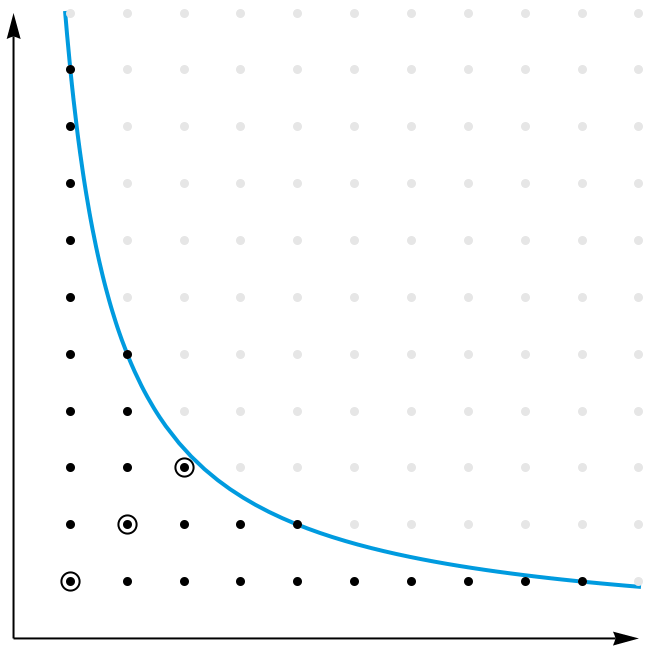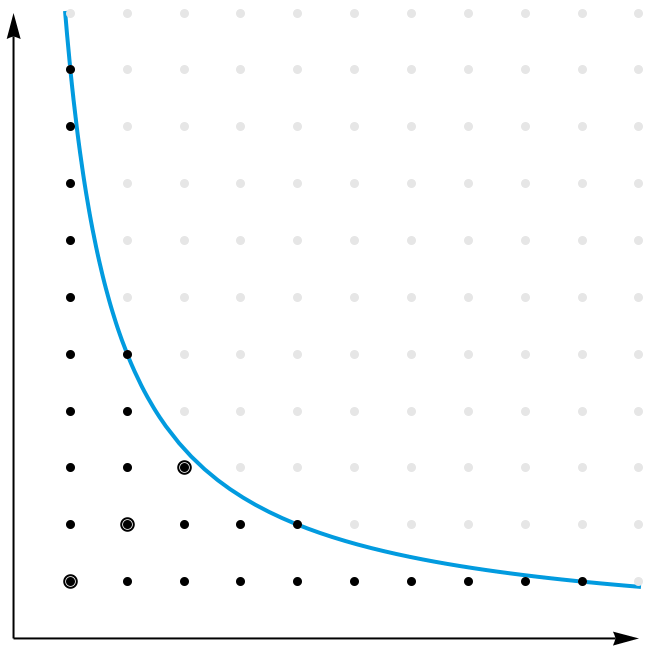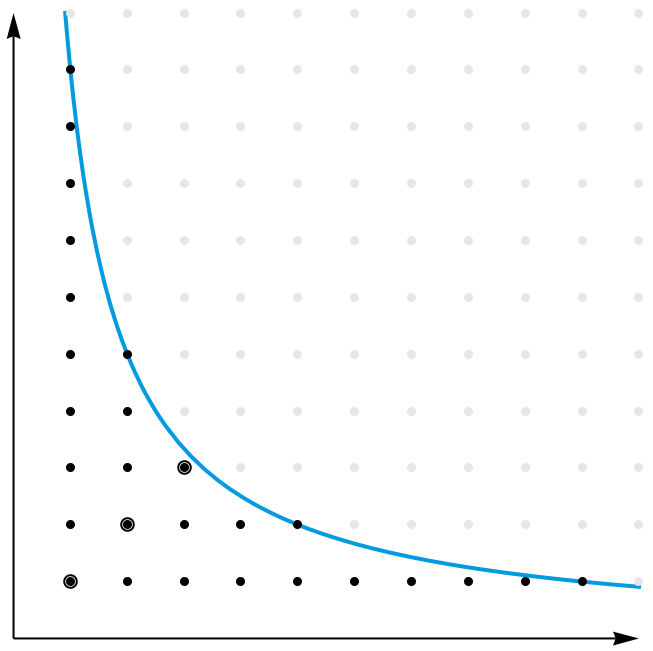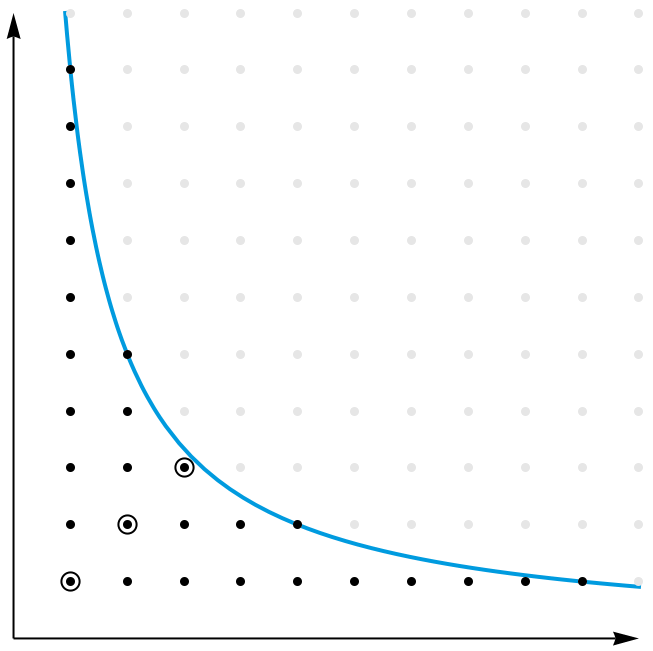
因此， [n/1] + [n/2] + [n/3] + … + [n/n] + [√n] 的值，其实就等于这两类点的总个数，其中后一类点被重复计算了两次。这个值显然应该是偶数。

题目来源：Cut-The-Knot

39 条评论

发表评论




Enter Captcha Here :