保加利亚单人纸牌游戏（Bulgarian solitaire）的玩法如下：

取出 45 张牌，然后把它们随意分成若干堆。接下来，从每一堆里各取一张牌，叠在一起形成一堆新的牌。不断这样做下去，如果某个时候桌面上正好有 9 堆牌，并且各堆牌数分别为 1, 2, 3, 4, …, 9 ，你就获胜了。

乍看上去，如果初始局面设定不佳，游戏很可能会陷入某个循环，从而永远无法获胜。然而， 1981 年，丹麦数学家 Jørgen Brandt 证明了，对于任意一个初始局面（包括把所有牌摆成 1 堆，以及把所有牌分成 45 堆这样的极端局面），游戏都能在有限步之内获胜。事实上，如果把 45 换成任意一个三角形数 n = 1 + 2 + … + k ，结论仍然成立。

在证明这个结论之前，大家不妨先来看两个例子。下图演示的是 n = 10 时的一种情形。我们把这 10 张牌分成了 (1, 3, 5, 1) 四堆，最终在第 6 次操作之后获得胜利。这里，我们用蓝色小圆点来表示扑克牌，并且规定新的牌堆总是加在原有牌堆的左边。

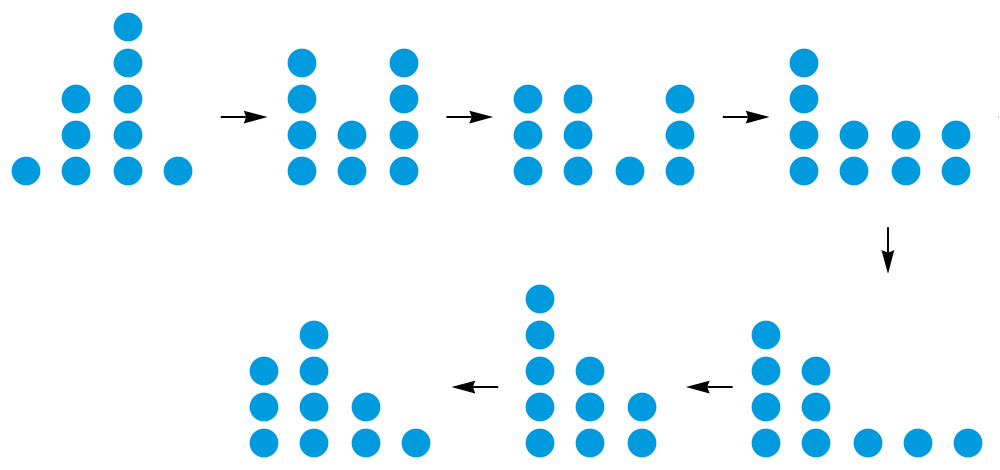
来看一个稍微复杂一些的例子吧。下图演示的是 n = 15 时的一种情形。我们把这 15 张牌分成了 (7, 8) 两堆，最终在第 14 次操作之后获得胜利。

 

 

 

 

 

 

 

 

 

 

我们无妨把每次操作等价地想象成下面这样。首先，把所有牌堆按照牌数多少从左至右排开，最左边那个牌堆的牌数最多，最右边那个牌堆的牌数最少。接下来，从最左边的那一个牌堆开始，依次从各个牌堆的最底下取出一张牌，并且叠成新的一堆，先取出来的放在下面，后取出来的放在上面。最后，把新的牌堆放在最左边。如果这个时候，它右边那个牌堆里的牌数更多，我们就要在此添加新的步骤：让它不断和它右边的牌堆交换位置，直到它右边那个牌堆的牌数和它相同或者比它更少。此时，牌堆再次变得有序，我们便可以重复刚才的过程，完成一次又一次的操作。按照这个约定，刚才的第一个例子，也就是 (1, 3, 5, 1) 那个例子，具体的游戏过程就变成了下面这样。我们把每一次构造新的牌堆和每一次交换两个牌堆都算作是单独的一步，于是整个过程一共有 7 步。

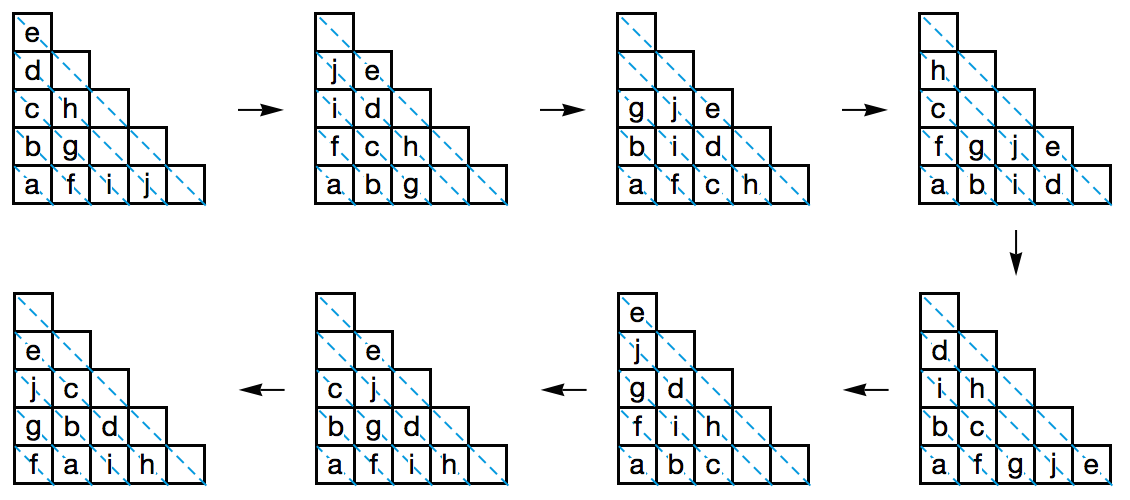
不断执行这样的操作，游戏局面将会逐次发生变化，得到一个又一个新的状态，最终必将会和之前的某个状态发生重复，此时便会产生循环。其中一种最简单的循环就是形如 (k, k-1, …, 2, 1) → (k, k-1, …, 2, 1) 的循环，这是一个长度仅为 1 的循环。接下来我们将证明，这是唯一可能出现的循环。

注意一个很有意思的事情：构造新堆的过程，其实就相当于是让每条对角线上的所有字母循环向下移动一位。例如，从第 1 幅图变到第 2 幅图，第 3 条对角线上的 c, g, i 就变成了 i, c, g ，第 4 条对角线上的 d, h, _, j 就变成了 j, d, h, _ 。所以，如果让每个字母都报出自己在第几条对角线上，再把所得的数字全部加起来，这个总和在构造新堆的前后是不会变化的。然而，每次交换牌堆的操作都会让这个总和严格地减小。具体地说，如果把牌数为 x 的牌堆与牌数为 y 的牌堆进行交换，那么在所有受到影响的 x + y 张牌中，有 2x 张牌会成对地左右互换位置，其余 y – x 张牌则会移动到前一条对角线上，于是所有字母所在对角线的编号之和将会减小 y – x 。这说明，在牌局变换的过程中，一旦出现了交换牌堆的操作，这个总和都会单向地减小，今后再也没法回到原来的水平。由此我们立即得出：一个循环里面绝不可能有交换牌堆的操作。

这意味着，在一个合法的循环中，所有的操作都是构造新堆的操作，本质上都是在循环移动各个对角线上的元素。下面我们来证明：在一个合法的循环当中，如果某条对角线上存在非空元素，那么它的前一条对角线上一定不能有空格。这是因为，如果第 i 条对角线上有某个字母 x ，并且第 i – 1 条对角线上有一个空格，那么经过 i – 1 步之后，这个空格会回到原位，此时 x 会出现在原位往上一格的位置（如上图的第 1 幅图和第 5 幅图，注意观察第 4 条对角线和第 5 条对角线）。不断这样下去，第 i 条对角线上的字母 x 一定会追上第 i – 1 条对角线上的那个空格，使得两者到达同一水平高度（即使刚开始两者所在的水平高度差异甚大）。这将会引发一次交换牌堆的操作（如上图中的第 7 幅图），而刚才我们已经说明了，一个合法的循环里不会出现交换牌堆的操作。

这说明，在一个合法的循环所涉及到的所有对角线当中，除了最外层的那条对角线以外，其余对角线必须都得填满。我们一共有 n = 1 + 2 + … + k 张牌，把这些牌按此要求进行摆放，可能性只有一种：依次填满第 1, 2, …, k 条对角线（如果要在第 k + 1 条对角线甚至更外层的对角线上填充元素，那么前面 k 条对角线必须被填满，牌数就不够了）。因而， (k, k-1, …, 2, 1) → (k, k-1, …, 2, 1) 就成了唯一可能的循环。

既然状态的演变过程中必然会产生循环，而 (k, k-1, …, 2, 1) → (k, k-1, …, 2, 1) 又是唯一可能的循环，于是我们就得到了本文最初提到的结论：一切初始状态最终都会变成 (k, k-1, …, 2, 1) 。

1983 年， Martin Gardner 在他的专栏上介绍了保加利亚单人纸牌游戏，随后又收录在了 The Last Recreations: Hydras, Eggs, and Other Mathematical Mystifications 一书中。我则是在 Algorithmic Puzzles 一书中看到的这个问题，上述证明方法也来源于此。