你知道吗？连分数

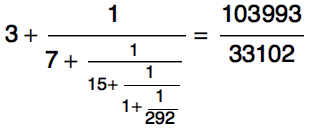
    而连分数

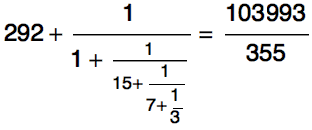
    这两个连分数的分子竟然是相同的！这是为什么呢？《Proofs that Really Count》里面给出了一个有意思的组合学解释。

    为了叙述方便，接下来我们统一用下图所示的符号来表示连分数：

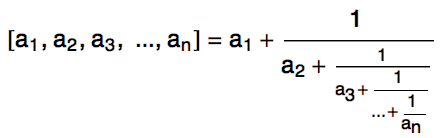
    我们用 p(a₁, a₂, a₃, …, a_n) 来表示 [a₁, a₂, a₃, …, a_n] 的最简分数形式的分子，用 q(a₁, a₂, a₃, …, a_n) 来表示 [a₁, a₂, a₃, …, a_n] 的最简分数形式的分母。于是，我们有

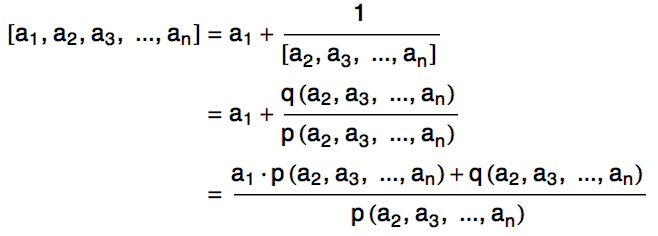
    注意到，最后的那个分数已经是最简的了。如果不是的话，这就意味着 p(a₂, a₃, …, a_n) 和 a₁ · p(a₂, a₃, …, a_n) + q(a₂, a₃, …, a_n) 之间有公共的因数，这进一步表明 p(a₂, a₃, …, a_n) 和 q(a₂, a₃, …, a_n) 之间必须要有公共的因数；然而 p(a₂, a₃, …, a_n) 和 q(a₂, a₃, …, a_n) 是 [a₂, a₃, …, a_n] 的最简分数形式的分子和分母，它们已经没有公共的因数了。

    因此，连分数的分母就应该满足

      q(a₁, a₂, a₃, …, a_n) = p(a₂, a₃, …, a_n)

    而连分数的分子则应该满足

         p(a₁, a₂, a₃, …, a_n)
      = a₁ · p(a₂, a₃, …, a_n) + q(a₂, a₃, …, a_n)
      = a₁ · p(a₂, a₃, …, a_n) + p(a₃, …, a_n)

    再结合初始条件 p(a_n) = a_n 以及 p(a_n-1, a_n) = a_n-1 · a_n + 1 ，我们就得到了连分数分子的一个完整的递推公式。接下来，我们要为这个递推公式赋予一个组合数学上的意义。考虑一个 n × 1 的棋盘，你可以在这个棋盘上放置一些 1 × 1 的砖块或者 2 × 1 的砖块。 1 × 1 的砖块可以叠放起来，但第 i 个位置上的砖块数目不能超过 a_i； 2 × 1 的砖块则只能单独放置，它的上面和下面都不能有任何别的砖块。我们规定，棋盘的每个位置上都必须放有砖块，不允许出现任何空的位置。假如 n = 6 ，并且 a₁ 到 a₆ 的值依次是 3, 1, 4, 1, 5, 9 ，那么我们的棋盘就如左图所示，右图则是一个合法的砖块放置方案。

    给定 n 的值以及序列 a₁, a₂, …, a_n 后，如何计算满足要求的砖块放置方案数呢？我们可以尝试着采用递推的办法。我们可以把所有的方案分为两大类。其中一个大类就是，第一个位置放有 1 到 a₁ 个 1 × 1 的砖块，这类方案的总数等于 a₁ 乘以在后面 n – 1 个位置放置砖块的方案数；另一个大类则是，第一个位置被一个 2 × 1 的砖块所覆盖，这类方案的总数就直接等于在后面 n – 2 个位置放置砖块的方案数。你会发现，这个组合问题的递推公式与刚才的 p(a₁, a₂, …, a_n) 完全一致，而且容易验证，只在第 n 个位置放砖块有 a_n 种方式，只在第 n – 1 和第 n 个位置放砖块则有 a_n-1 · a_n + 1 种方式，这也与 p(a_n) 和 p(a_n-1, a_n) 的值是相符的。因而， p(a₁, a₂, …, a_n) 的值正好就是在高度限制分别为 a₁, a₂, …, a_n 的棋盘上放置砖块的方案总数！

    回到本文最初的问题：为什么连分数 [a₁, a₂, a₃, …, a_n] 和 [a_n, …, a₃, a₂, a₁] 的分子是相同的呢？现在看来几乎是显然的：因为这两个连分数的分子表示的是两个左右镜像的棋盘的砖块放置方案数，而两个左右镜像的棋盘本质上是相同的，它们的砖块放置方案数显然应该相等。