大家在吃饭喝酒时是否注意到了这样的事情：三个人碰杯时，每个人的杯子都能同时和其他两个人的杯子相接触，很完美；但是四个人碰杯时，任一时刻总会有两个人碰不到杯，非常尴尬。有一次和三个好朋友吃饭，四人碰杯时又发生了这种尴尬的情况，突然有一个人异想天开，把他的杯子放到了另外三个杯子的上面，从而实现了四个杯子两两接触！我们自然引出了这样一个问题：如果 n 个全等的圆柱体两两相接触，则 n 最大是多少？
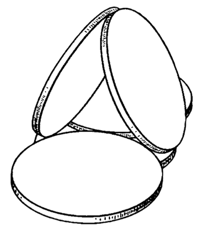
对于不同形状的圆柱体，答案可能是不一样的。 Martin Gardner 在 Hexaflexagons and other mathematical diversions 一书中提到，我们可以精巧地摆放 5 枚硬币，使得它们两两相接触，如上图所示（注意，最底下还藏着一枚硬币）。同时， Martin Gardner 问到，能否摆放 6 支香烟让它们两两接触？一个经典的答案如下：
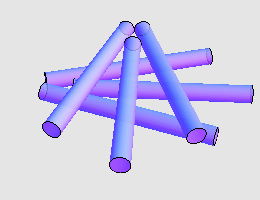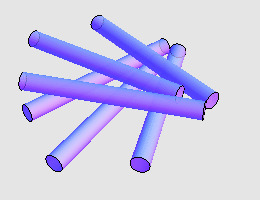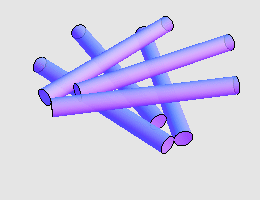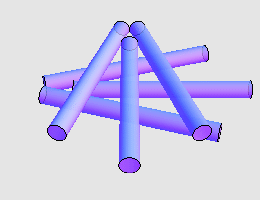
令 Martin Gardner 本人也感到吃惊的是， George Rybicki 和 John Reynolds 指出， 7 支香烟两两接触也是有可能的。他们给出的构造如下：
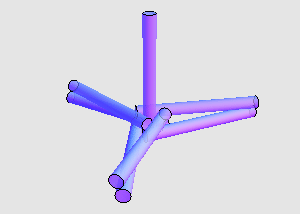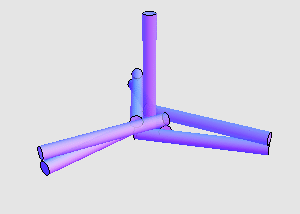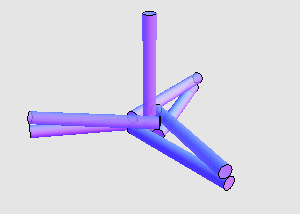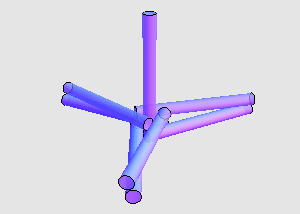
两两接触的全等圆柱体最多可以有多少个？ 7 个已经是最多的了吗？如果圆柱体的高度与半径之比有所限制，这会对问题的答案产生怎样的影响？这些问题都还有待解决。
1968 年， John Littlewood 提出了这样一个问题：在空间中，是否存在 7 个单位半径的无限长圆柱体，使得它们两两相接触？这个问题显然更难一些，因为我们没法利用圆柱体的顶面和底面了。
根据 MathPuzzle 的消息，最近， Sándor Bozóki 、 Tsung-Lin Lee 和 Lajos Rónyai 解决了这个问题。他们建立了一个非常非常庞大的方程组，里面有 20 个未知数以及 20 个方程：
通过某些数值计算方法，他们得到了两组不同的解。其中一组解如下：
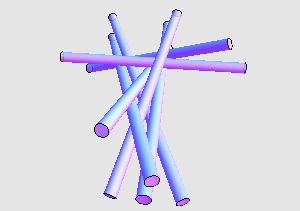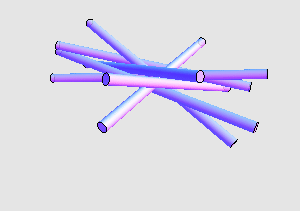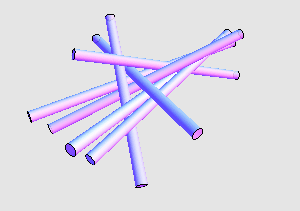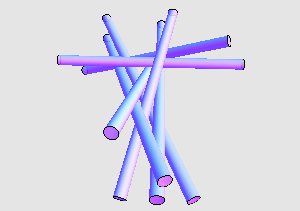
下面则是另外一组解：
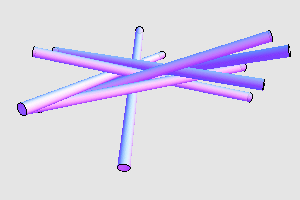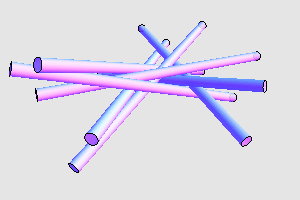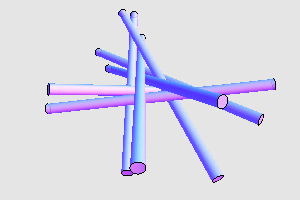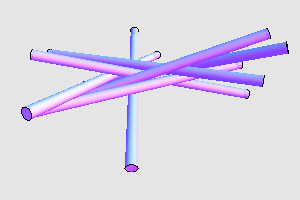
2005 年， András Bezdek 证明了任意 25 个无限长的等粗圆柱体中，总存在两个相离的圆柱体，从而说明了满足要求的圆柱体数目 n 存在一个上界。那么， n 的最大值是否就是 7 呢？这个问题目前也没有定论。
已阅。
已阅
好有趣的研究。。。。
图是啥工具画的？不错
前排！抢位子！
我很好奇做出模拟图的软件
作图是Mathematica？
没想到此题如此之难。
虽然，用方程的方法得到了这么一个结果，但方法并不优美。也许很难找到一个更好的办法吧。
这个太牛了~
好基的题目啊。
方程式怎么计算的呀，二十几个呢?
^_^，果然是来自于生活的数学啊，研究这样的问题，很不一样
图是咋做的？？？？
应该把这篇文章给那四个喝酒的人中的剩下三个看……
生活中随便找出一个数学问题都如此难解，果然人类对于数学还是一知半解…… 以后还有很长的路要走……
那个方程组的未知数是代表什么？
是不是如果平面内，能5个平面图形，两两相接，则4色定理不成立。
有本书上说了类似的。我今天才知道。
三人能碰杯四个人不能碰杯（普通的那种）是和四色问题的基本上是一致的思路，都是平面问题．
真是腻害
本来以为六个已经是极限…没想到….
学习了，不简单呀