请你把一个圆形的比萨分成若干个大小形状都相同的部分，使得其中至少有一部分不含有比萨的边儿。换句话说，你需要把一个圆分成若干个全等的部分，其中至少有一个部分不包含任何一段圆周。
答案：如图，首先用 6 条同样半径的 1/6 圆弧把整个圆分成 6 个形如鱼尾的全等图形，然后再沿着对称轴把每个鱼尾分成两半即可。这样，我们便把整个圆分成了大小形状都相等的 12 个部分，其中 6 个部分都不含有任何一段圆周（虽然有一个点在圆周上）。
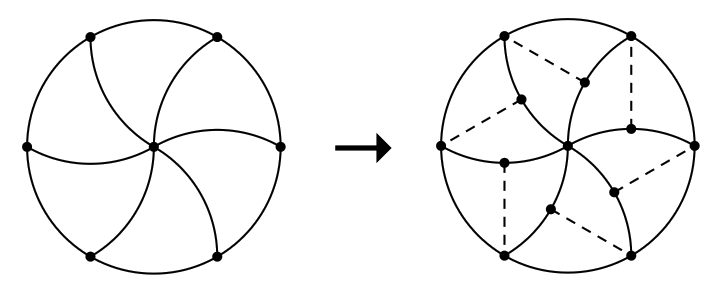
在这种方案中，分出来的 12 个小块虽然都是全等的，但其中某些小块需要经过翻折后才能彼此重合。我们的下一个问题就是：请你再设计出一种圆的分割方案，使得每个小块都全等，至少有一个小块不含边，并且所有小块都可以仅通过旋转和平移就能与其他小块重合。
答案：如图，首先用 12 条同样半径的 1/6 圆弧把整个圆分成 12 个全等的图形。这说明，刚才的每个鱼尾形都还有另一种平分方案。现在，把每个鱼尾形翻过来摆放，就得到满足要求的方案了。
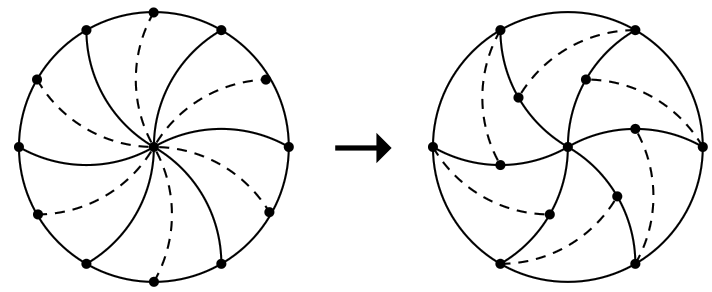
题目来源：http://math.stackexchange.com/questions/481527/slice-of-pizza-with-no-crust
已阅。
这是发完了就M老婆说我写了新博文的暗示么→_→
好巧妙~
PS:赞板凳君慧眼如炬！
求M67牛来新加坡访问……顺便虐一下坡上人群。
（才不告诉你我今年16看了你的网站3年）
好玩
2012年青少年數學國際城市邀請賽(IWYIMC)
團體賽的第七題與這個有點像
它題目是要分做全等的部分
但是最少有一份是(邊界和內部都)不包含圓心的
然後上面有其中的兩種解答
赞一个
orz
这个让我想到了，电影里发射火箭时的天窗……
能否请教一个无聊的问题。一个九宫格，第一排的第三个元素为21，第二排的第三个元素为6，第三排的第二个元素为13。现需要将其他格子填上数字，使得横竖斜相加或相减都等于45. 不知道这个填数字问题有没有技巧呢。请大神指导。
请问，只有一种方案吗？
若干个是不限定多少个吗？那两个也算？
这不是说只要找到√2/2半径长度再画个内同心圆就ok了？
这应该很简单啊。
而且，貌似用尺规做出√(i/n)也不是很复杂，这样通过画同心圆就能做任意等分了。
这些解似乎都太“平凡”了，有没有一种办法不但满足这个条件，而且使圆心必须在其中一块上，而不是作为一个点被几块共用？
不错
楼层: 14楼 | 2013-09-15 14:00 | morrowind 说：
若干个是不限定多少个吗？那两个也算？
这不是说只要找到√2/2半径长度再画个内同心圆就ok了？
这应该很简单啊。
而且，貌似用尺规做出√(i/n)也不是很复杂，这样通过画同心圆就能做任意等分了。
注意不光是面積相同，要求形狀也一樣呀
第二问中首先分为的12小块，这样不是每一块都含有饼边了啊。感觉不符合题目要求了。
楼层: 18楼 | 2014-01-02 14:37 | Craig 说：
第二问中首先分为的12小块，这样不是每一块都含有饼边了啊。感觉不符合题目要求了。
作者只是证明了这样分割的12个图形是全等的。你可以直接把饼分成第二张图那样~
第二问中首先分为的12小块
请问，只有一种方案吗？
可不可以先取出半徑的三分之一的小圓pizza,剩下的環狀再分成8份。
小圓pizza加油為所求！可以嗎？
有没有连点都不在边上且旋转全等的方案？