证明：对于平面上的任意一个大小为 10 的点集，我们总能在平面上不重叠地放置若干个单位圆，使得它们合起来可以覆盖到所有这 10 个点。
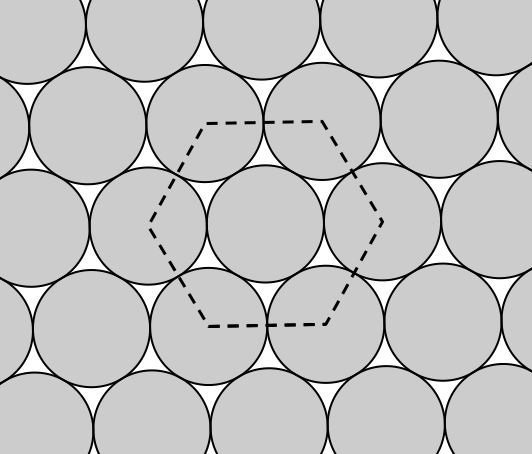
让我们先把充分多的单位圆放在平面上，并像上图那样紧密地排列在一起，则它们将覆盖这个平面 π / (2 · √3) ≈ 0.9069 的面积。这是因为，整个图形可以看作是由虚线所示的正六边形平铺得来的，而每个正六边形的面积为 6 · √3 （六个边长为 2 的等边三角形），其中被覆盖的部分正好可以拼成三个完整的单位圆，其面积为 3 · π ，占整个正六边形的 (3 · π) / (6 · √3) = π / (2 · √3) ≈ 0.9069 。
不过，这并不能保证点集中的每个点都被这组圆覆盖到了。现在，随机地对这组圆进行平移，得到一系列概率均等的圆盘放置方案。在这些圆盘放置方案中，每个点都有 0.9069 的概率被覆盖到，换句话说每个点被覆盖到的期望次数都是 0.9069 ；因此，在这 10 个点中，发生覆盖的期望次数就是 9.069 ，这是一个大于 9 的数。那么，这里面一定有一种圆盘放置方案，它至少产生了 10 次覆盖，这就表明所有的 10 个点都被覆盖到了。
已阅。
我是来拜楼上localhost姐姐的。。
localhost是谁呀= =
wow, localhost!
久违的更新
如果概率小于9或有十一个点该怎么办呢，原命题不成立吗
我感觉这个证明不对。。。
单个点被覆盖的概率是0.9069没问题，但各个点被覆盖应该不算是独立事件，所以不能直接拿0.9069乘10吧？
你可以看成是先放好圆，再选出那十个点
哈哈，这个证明不错。
非构造性
似乎不能证明采用是有限个圆啊？
to xycben:
去掉没用的圆就是有限个了
那么11个该怎么构造呢？
博主，你好，你在博客中是如何编辑数学符号的，博客是用什么专门的软件编辑的吗？
To:Garrus
证明没问题的，这个事件是服从二项分布的，所以最终期望就是n*p，n是10，p是0.9069
最后一步的证明太漂亮了!
感觉Garrus 是有道理的，每一种构造，这n个点都是相关的，并不独立。如果存在一种构造，当某k个点被覆盖时（k>=2），一定存在一个点不能被覆盖，就不能这样计算期望值，如果证明以上构造不存在，这道题也就证明了，不用再算什么期望值了。
E(X+Y)=E(X)+E(Y)
这个式子天然成立，不以相关性为前提的。期望是可以这么算的～
谢谢15楼，是我对期望计算理解有错
妙证总让人觉得有点逻辑站不稳，要不然也不会有这么多人有疑问了。我想知道这道题的常规证明应当怎么做？
看不懂你博客的人,也迟迟等不到你的keywords了.
我是来拜localhost姐姐的。。
15楼不对啊，不能是X+Y.应该是XY
最後一步是鴿籠原理？
发生覆盖的期望“个数”就是 9.069 。吧
回复20L 你可以把0.9连续加10次……….这里乘的10是常数又不是概率。
好巧妙的证明
漂亮啊！这个题目是属于让人心中一亮的：咦，竟然还能这样来证明。
如果没有一个覆盖方案能做到，那概率是不可能超过0.9的，这就足够强了。
证明有问题。希望博主三思。
对于一个点，博主的期望是算对的。
对于i.i.d的10个点，博主的期望也是算对的。
但对于精心构造的10个点来说，不能当作随机变量来看。
比如说，我构造三个点：博主图中的切点可构成的最小的等边三角形（不画图好难描述）。
这三个点不可能被同时不被覆盖（几何原因）。 但是按照博主的逻辑这三个点都不被覆盖的概率＝（0.0931)^3>0
好机巧的证明。但这个好像不是概率题吧。
楼上一群说可能不独立的人能不胡闹了吗。。。
用二重积分来代替概率也可以，你们好好想想
test