日常生活中经常会出现这样的场景：你想在数据库上查询某个东西，但却不希望留下线索，让别人知道你查询了什么。比方说，投资人可能会在数据库上查询某支股票的信息，但却不希望任何人知道他感兴趣的股票究竟是哪一支。看上去，似乎唯一的办法就是把整个数据库全部拷回家。然而，这些数据往往都拥有非常庞大的体积，全部拷走通常都是很不现实的；另外，考虑到数据内容的隐私性和数据本身的宝贵价值，数据的持有者通常也不允许其他人把整个数据全盘拷走。不过，随着分布式数据库的广泛应用，上面的难题有了一个两全其美的好办法：假设有两个内容完全相同的数据库，投资人可以先在第一个数据库上执行一个不会透露目的的查询，再在另一个数据库上执行另一个不会透露目的的查询，两次查询结合起来便能推出想要的结果。只要没有人刻意去收集并且对比两个数据库的查询记录，那么谁也不会知道投资人真正想要查询的是什么。在这个背景下，我们有了下面这个有趣的问题。

    服务器随机产生了一个 {1, 2, …, 100} 的子集 S ，并且同时发送给了 A 和 B 两名前台工作人员。 A 、 B 两名前台都接受其他人的提问，但为了保护数据，两个人都只能用“是”或者“否”来回答问题，并且都不允许同一个人重复提问。你非常关心某个数 n 是否在这个子集里。其实，你本来可以直接问 A 和 B 中的任何一个人“数字 n 是否在集合 S 里”，但是这样一来，对方就知道了你想要查询的是什么。为此，你可以向 A 和 B 各问一个问题（结合两人的回答便能推出集合 S 里是否包含数字 n ），但却不能让 A 和 B 当中的任何一个人知道你查询的是哪个数（我们假设 A 、 B 两人不会串通起来，把他们各自收到的问题联系在一起）。事实上，你需要保证 A 和 B 两人都不能从你的问题中获取到任何信息，也就是说，对于 A 和 B 当中的任何一个人来说，各种问题出现的概率不会随着 n 值的改变而改变。再换句话说，如果 n 的值变了，那么 A 和 B 各自将会听到的问题应该拥有和原来相同的概率分布。

    答案：首先，自己随机生成一个 {1, 2, …, 100} 的子集 T₁ （每个数都有 1/2 的概率被选进 T₁ ）。如果 T₁ 里面正好包含数字 n ，那么就把 T₁ 里的数字 n 去掉，把所得的结果记作 T₂ ；如果 T₁ 里面没有数字 n ，那么就在 T₁ 中加入数字 n ，从而得到 T₂ 。现在，将 T₁ 发送给 A ，并询问 T₁ 里面是否有偶数个数正好也在 S 里。类似地，再将 T₂ 发送给 B ，并且询问同样的问题：在 T₂ 里面是否有偶数个数同时也属于 S 。注意， T₁ 和 T₂ 的唯一差别，就是一个里面有 n 一个里面没有 n 。因此，如果 A 和 B 的回答是一致的，就说明数字 n 不在 S 里面；如果 A 和 B 的回答不一致，就说明数字 n 在 S 里面。另外，容易看出，不管是 T₁ 还是 T₂ ，从 1 到 100 每个数在里面出现的概率都是 1/2 。因此，不管是 A 还是 B ，他被问到的问题都总是具有完全相同的概率分布，这不随 n 的变化而变化。

 
 
    这种方案的缺陷就是，每条询问都非常长。为了描述 T₁ 或者 T₂ ，我们需要使用一个 100 位的 01 串，它一共有 100 个 bit 。如果 S 不是 {1, 2, …, 100} 的子集，而是 {1, 2, …, N} 的子集，那么在上述方案中，我们需要给 A 、 B 各发送 O(N) 个 bit 的数据。在 N 非常大的情况下，这么做同样是不现实的。有趣的是，如果前台不止两个人，而是四个人的话，那么我们可以做得更好：我们可以给四个人都只发送 O(√N) 个 bit 的数据，并且同样保证每个人都不能从中推出任何信息来。

    为了便于说明，我们现在假设 S 是 {0, 1, 2, …, 99} 的一个子集。假设你想要知道， 67 是否在集合 S 里。于是，你首先随机生成一个 {0, 1, 2, …, 9} 的子集 T₁ ，然后在里面加上数字 6 （如果 T₁ 里没有 6 的话）或者去掉数字 6 （如果 T₁ 里有 6 的话），得到 T₂；再生成另一个 {0, 1, 2, …, 9} 的子集 T₃ ，然后在里面加上数字 7 （如果 T₃ 里没有 7 的话）或者去掉数字 7 （如果 T₃ 里有 7 的话），得到子集 T₄ 。接下来，向 A 、 B 、 C 、 D 依次询问下面四个问题

      A ：在所有十位数属于 T₁ 并且个位数属于 T₃ 的数当中，是否有偶数个数在集合 S 里。
      B ：在所有十位数属于 T₁ 并且个位数属于 T₄ 的数当中，是否有偶数个数在集合 S 里。
      C ：在所有十位数属于 T₂ 并且个位数属于 T₃ 的数当中，是否有偶数个数在集合 S 里。
      D ：在所有十位数属于 T₂ 并且个位数属于 T₄ 的数当中，是否有偶数个数在集合 S 里。

    如果 T₁ 等于 {2, 4, 7, 8, 6} ，那么 T₂ 就应该等于 {2, 4, 7, 8} ；如果 T₃ 等于 {2, 3, 5} ，那么 T₄ 就应该等于 {2, 3, 5, 7} 。四次询问之后我们便可得知，在下图各种颜色的方框中，属于集合 S 的数有奇数个还是偶数个。结合 A 、 B 的回答（蓝色方框和黄色方框），我们就能推出，在集合 S 当中，十位数属于 T₁ 并且个位数恰好为 7 的数有奇数个还是偶数个；结合 C 、 D 的回答（红色方框和绿色方框），我们就能推出，在集合 S 当中，十位数属于 T₂ 并且个位数恰好为 7 的数有奇数个还是偶数个。于是，我们就可以知道，十位数恰好为 6 并且个位数恰好为 7 的数是否在集合 S 当中了。

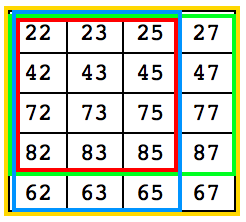
    类似地，如果集合 S 是 {1, 2, …, N} 的子集，那么我们可以对这 N 个数进行重新编码，使得每个数都由高位和低位组成。那么，高位和低位的取值范围都是从 1 到 √N 。在整个协议中，我们需要给每个人发送两个 {1, 2, …, √N} 的子集，这相当于两个 √N 位的 01 串，因此其数据量为 2√N 个 bit ，也就是 O(√N) 个 bit 。

    不过，请注意，虽然与每个人交流的数据量少了，但这次却有四个人了，因而你需要发送四个这么大的数据。当 N 很小的时候， 4 · 2√N 很可能反而比 2 · N 更大。

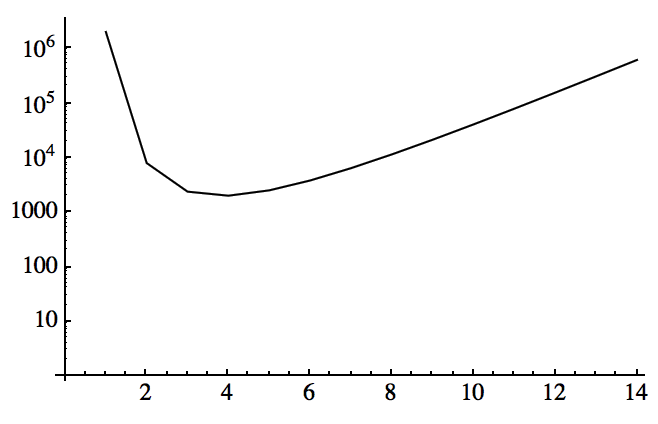
    同样地，如果我们有 2^d 个人，我们就可以把 1 到 N 里面的所有数都看作 d 位数，每一位的取值范围是从 1 到 N^1/d 。为了完成一次查询，我们需要给每个人发送 d 个 {1, 2, …, N^1/d} 的子集，因此总共需要发送 2^d · d · N^1/d 个 bit 。对于不同的 N ，我们可以选取最合适的 d ，使得 2^d · d · N^1/d 最小。例如，下图所示的就是 N = 1 000 000 时函数 f(d) = 2^d · d · N^1/d 的图像，可见 d = 4 时的通信成本是最低的。因此，如果查询点足够多的话，我们可以选择在 16 个不同的地方进行查询。

参考资料： B. Chor, O. Goldreich, E. Kushilevitz, M. Sudan, Private Information Retrieval, Journal of the ACM (JACM), 1998