下面是趣题集 Which Way Did the Bicycle Go 中的第 71 个问题。如下图，在这个六边形的围墙中，如果站在图中圆点的位置，那么有两面墙不能被完全看见（其中一面墙完全看不见）。能否设计出一个多边形围墙，使得站在围墙里面的某个地方后，所有的墙都至少有一部分是不可见的？
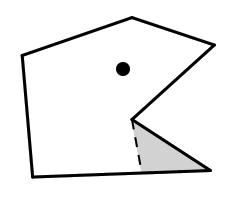
是的，如下图。真正有趣的是， Which Way Did the Bicycle Go 一书上还给了一个附加题：能否设计出一个多边形围墙，使得站在围墙外面的某个地方后，所有的墙都至少有一部分是不可见的？继续阅读下去前，不妨先想一下。
是的，如下图。你花了多少时间才想到了这一招？在可见性问题的研究中，这是一种很常用的技巧。
似乎看过。。追了几年之后，第一次评论貌似是沙发？
终于更新了，工作之余来瞅瞅。
额，两个问题一个也没想出来
总感觉解的很恼人……
第一个问题，多边形的最小边数是多少呢？ 风车的形状，六边形就可以满足条件，感觉不能再小了。。。
不知道能否证明五边形是不行的，也就是五边形内任一点，都能看到至少一条完整的边？
问得好……
考虑四边形的情况，易得四边形内任意一点至少可看到两条完整边。那么只需考虑能否将其中一条边折断（四边形变为五边形）并遮挡这两条边。似乎是不可能的
受石器的启发，想到了三角剖分，完成了这个证明（五边形不行）
显然，对于某个多边形，如果存在三角剖分方案，使得每个小三角形至少有一条边是多边形的边，那么多边形内的任一点，都至少能看到多边形的一条完整的边。（反命题不知道是否成立。。。）
在这个引理的基础上，只要证明对于任意五边形，都存在三角剖分，使得每个小三角形都至少有一条边是多边形的边。这个结论是显然的，因为五边形的任何三角剖分，都满足这个条件。
关于算账提到的反命题，在多边形内每一条边对应一个点集，其中每个点都能看到这一整条边。那么这个问题就变得更复杂了。捣乱完毕，走人。
前一张是老图，后一张。。。。。
五边形可以构建，四边形不行。
五边形，M字型下面加一横就可以。
哈哈的确没想到
1232123abcde
233 后一种想到了
如果问题是构造一个多边形使得多边形(外)的一点无法看全任意一边，是否有解？