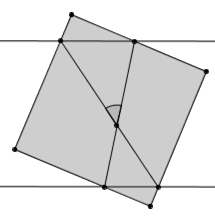
如图，把边长为 d 的正方形放在两条距离也为 d 的平行线之间，于是产生了四个交点。求证，把这四个点交叉相连产生的夹角为 45° 。
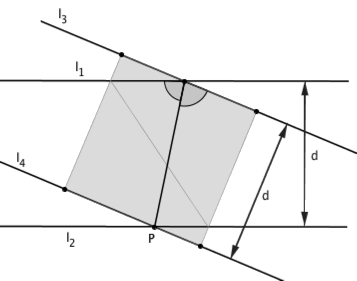
只需要注意到，如果两条距离为 d 的平行线之间夹着一条线段，那么这条线段的长度唯一地确定了它与两条平行线的夹角。因而，下图中所标注的两个角的度数显然相等（我们也可以严格地证明这一点，只需要过点 P 分别作 l1 和 l3 的垂线段，并证明三角形全等即可）。
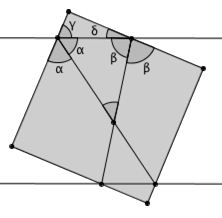
所以，在下图中，两个标有 α 的角是相等的，两个标有 β 的角也是相等的。接下来就简单了。由于 γ + δ = 90° ，并且 2α + 2β + γ + δ = 360° ，因此 2α + 2β = 270° ， 即 α + β = 135° 。那么，我们要求的角度就是 180° – 135° = 45° 了。
题目来源： http://www.mathteacherctk.com/blog/2013/05/a-square-in-parallel-lines
已阅。
沙发
前排~~
好神奇
補充一下，是中心重合的兩個全等正方形。
語病甚麼的就不要吐槽了。。。
地下室！！~
中学数学证明题。
命题的条件有点不够严谨吧，考虑极端的情况，正方形有一对平行的边正好与给定的两条平行线重合，此时产生的四个交点就是正方形的四个顶点，而正方形的对角线夹角是90度
LS你说得那样有无穷多个交点。。。不是4个
看着题目，总是想画个圆怎么破？
已看过，留下痕迹
观察真仔细。。
这样的论证也太神奇咯
好题，巧妙地利用了两个距离相等的平行线的夹角相等。
漂亮。
真神奇
顾大神，我想问个问题，你的图形都是用什么画出来的
哪有什么神奇的，正方形只是个幌子，其实中间的交叉线的任何一根，都其实只是由两组间距为d的平行线所决定，而两组间距相等的平行线组成的图形其实就是个菱形，对角线当然平分该角。
更一般点，就是3组间距为d的平行线A,B,C，AB和AC所确定的交叉线夹角为α，BC的夹角为β，那么α和β满足：2α+β=180.
如上，此题中α=45，β=90
其实第二个图不用证全等，角度转换就行了，直线180°
这个也还好吧，没什么神奇的。两个等距离的平行线中间形成了一个菱形。那条线刚好是菱形的对角线。
巧妙