证明：对于任意一个三角形和任意一个大于等于 4 的正整数 n ，都存在一种把这个三角形分割成 n 个等腰三角形的方案。这个问题曾经出现在 1976 年的 Crux Mathematicorum 上。 1977 年， Gali Salvatore 给出了一个非常漂亮的解答。
首先，让我们来看一看如何把任意一个三角形分成 4 个等腰三角形。如图，作出三角形的高，把整个三角形分成两个小直角三角形。对于每一个直角三角形，作出斜边上的中线后都将会把它分成两个小等腰三角形。于是，我们就把整个三角形分成了 4 个小等腰三角形。
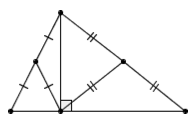
我们借此还能实现，把任意一个三角形分成 7 个等腰三角形：只需要先把它分成 4 个等腰三角形，然后再次套用上述方法，把其中一个小等腰三角形继续细分成 4 个更小的等腰三角形即可。事实上，我们还可以继续这样做下去，从而让等腰三角形的数目 3 个 3 个地增加。因此， n = 4, 7, 10, 13, … 的情况便全部解决了。
由于我们可以让任意分割方案中的等腰三角形数目加 3 ，因而如果 n = 5 和 n = 6 的情况也解决了， n = 5, 8, 11, 14, … 和 n = 6, 9, 12, 15, … 的情况也都自动地解决了，结论也就证到了。所以，接下来我们只需要考虑 n = 5 和 n = 6 的情况。
n = 6 的情况非常简单，如图，只需要把三角形分成两个直角三角形，再把其中一个直角三角形继续细分成两个更小的直角三角形，最后作出三个直角三角形各自斜边上的中线即可：
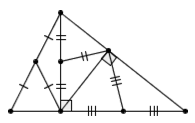
n = 5 的情况呢？我们有一个妙招：先在三角形里边分出一个等腰三角形来，然后把剩下的那个三角形分成四个小等腰三角形：
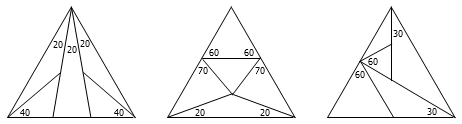
但是，上面这招有一个缺陷：它不能用于等边三角形。为了从原三角形中分出一个等腰三角形来，我们需要在某条边上截取一段，使得它等于另外一条边的长度。但是，如果三角形的三条边全都一样长，这一点就做不到了。因此，我们必须单独为等边三角形想一种把它分成 5 个等腰三角形的方案。好在这并不困难，我们有很多种办法，比方说，像下图这样：
Which Way Did the Bicycle Go 一书中给出了更多不同的把等边三角形分成 5 个等腰三角形的方案：
至此为止，问题就全部解决了。
参考资料：Ross Honsberger, From Erdos to Kiev: Problems of Olympiad Caliber, pp. 13-17
支持！沙发！
有意思
看题目不知从何下手，这个解题妙就妙在分成n=4,5,6
也可以这么证：
1）任意三角形都能被分成 n>=2 个直角三角形
2）任意直角三角形都能被分成2个等腰三角形
3）任意直角三角形都能被分成3个等腰三角形
只有3）的证明稍微复杂一点。对于非等腰直角三角形，可以在长直角边上找到一点，和对角连线，分割成一个直角三角形和一个等腰三角形，再套用2）即可；对于等腰直角三角形，先等分再等分，即可分为三个等腰（直角）三角形。
最后，n>=2个2或者3，显然可以相加得到n>=4的任何数
怎样证伪n=3,n=2 ?
这样的三角形就不是任意的了，有条件限制：直角三角形可以，一个角是另一个角的2倍的三角形（小角要小于45度）可以，一个角是另一个角的3倍也可以
好评
一定要在地核之前呀~~~
我怎么已经在地核里面了…！
那我在哪里捏…
@地下室 正三角形就不行。很简答的分类讨论。
不错。。。
10楼 @Raman
正三角形连接中心与3个顶点即可分为3个等腰三角形，所以只能证伪n=2。
@12楼 没错，是我疏忽了……只想着先切成两个再切一下变3个这种方法了，忘了中间一点连三条线这种了。这样的话任意锐角三角形只要找到外心就可以了。直角三角形也很好找到办法。那就只能从钝角三角形着手了。等腰钝角三角形也容易做出，所以只能找不等腰的了。
可以证明对于比较扁的不等腰钝角三角形的话，比如变长1,2,2.999这种，内部一点连出来三条线这种是搞不定的。其他方法就只有切成俩三角形然后再切一下变成3个这样了，这种情况必须保证第一下就要先切出一个等腰三角形，然后再把剩下那个切成俩等腰三角形。然后不管怎么切，对于刚才说的很扁的不等腰钝角三角形，切出来一个等腰三角形之后剩下的肯定还是个钝角三角形。再一下要把钝角三角形切成两个等腰三角形，这样的钝角三角形必须满足三个角度里某两个有个3:1的关系，这个要求不是随意就能达到的，实际上估算下就知道1,2,2.999这样的组合就没法搞出3:1的比例。所以还是不行的。
呃，除了3:1还有2:1。反正换成4,5,8.999也行，总之角度恰好满足要求的是巧合，一般是凑不出来的就是了。
怎样的三角形能分成三个等腰三角形呢？这个集合的完整刻画是什么
h ttp://blog.wolfram.com/2013/03/28/from-close-to-perfect-a-triangle-problem/
也是三角形剖分，正方形能被分成最少幾個45-60-75的三角形。藉由MMA，由數值方法突然轉成精確解，神乎。
让等腰三角形的数目 3 个 3 个地增加。因此， n = 4, 7, 10, 13, … 的情况便全部解决了。http://www.qireyi.com
我想了一个解法：
（1）任何一个三角形可以分成4个等腰三角形；
（2）任何一个三角形可以分成两个三角形，其中一个是等腰三角形；
（3）结合1,2，则任何一个三角形可以分解成n>=4个等腰三角形。
问题是，第2步，也就是文中的第3幅图，怎么证明呢？如何证明一个三角形总能分出一个等腰三角形呢？
貓咪大戰爭六周年