趣题：一个与含60度的三角形有关的性质

      

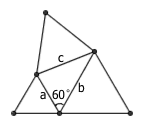
    有一个三角形，三边长分别为 a 、 b 、 c ，其中 a 、 b 两条边夹角为 60° 。分别以 a 、 b 、 c 为边向外作等边三角形。求证：前两个等边三角形的面积之和，减去第三个等边三角形的面积，将等于原三角形的面积。


 
 
 
 
 
 
 
 
      

    我们提供两种方法。一个容易想到的传统做法便是，利用余弦定理求出 a 、 b 、 c 之间的关系。由于 c 所对的角是 60° ，因此有：

      2 · a · b · cos60° = a2 + b2 – c2

    由于 cos60° = 1 / 2 ，上式化简为：

      a · b = a2 + b2 – c2

    另外，由于 sin60° = √3 / 2 ，因此我们在上式左边乘以 (1 / 2) sin60° ，在等式右边乘以 √3 / 4 ，等式仍然成立：

      (1 / 2) · a · b · sin60° = (√3 / 4) a2 + (√3 / 4) b2 – (√3 / 4) c2

    注意到边长为 s 的等比三角形面积公式为 (√3 / 4) s2 ，另外等式左边的 (1 / 2) · a · b · sin60° 正是原三角形的面积，于是命题得证。

 
 
 
 
 
      

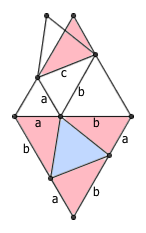
    我们给出另一种看起来更帅的做法，能够更直接地得到这个结论。容易证明，图中的水平线段 a 和水平线段 b 确实是在一条直线上，它们共同组成了一条长为 a + b 的线段。像上图那样，以这条长为 a + b 的线段为边，作一上一下两个大等边三角形。不难看出，所有的红色三角形都跟原三角形全等，而这又能推出，蓝色三角形就是一个边长为 c 的等边三角形。如果把原三角形的面积记作 X ，把边长为 s 的等边三角形的面积记作 A(s) ，于是有 A(a) + A(b) + 2 · X = A(a + b) = A(c) + 3 · X ，整理可得 X = A(a) + A(b) – A(c) ，命题得证。

题目来源：http://www.cut-the-knot.org/Curriculum/Geometry/GeoGebra/Eutrigon.shtml

23 条评论

发表评论




Enter Captcha Here :