五个有趣的拓扑变换问题

    如果你喜欢上次的空间想象能力挑战，你一定会喜欢 V. V. Prasolov 的 Intuitive Topology 一书。书中的第一章有五个非常经典的“拓扑变换”类谜题，在此与大家分享。注意游戏规则：我们假设所有物体都是用橡胶做成的，可以随意地拉伸、挤压、弯曲，但不允许切断、粘连等任何改变图形本质结构的操作。

    1. 能否把左图连续地变形为右图？

      

 
    2. 能否把左图连续地变形为右图？

      

 
    3. 左图所示的立体图形表面画有一个圆。能否通过连续变换，把这个圆变到右图所示的位置？

      

 
    4. 在一个轮胎的表面上打一个洞。能否通过连续变换，把这个轮胎的内表面翻到外面来？

      

 
    5. 能否把左图连续地变形为右图？

      

 
 
 
 
 
 
 
 
 
 
 
 
 
    1. 能否把左图连续地变为右图？

      

 
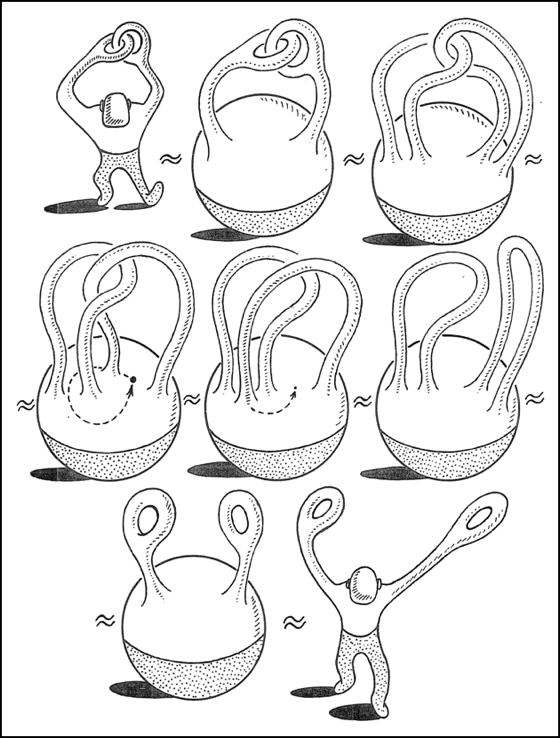
    答案是可以的，如下图所示：

      

 
    这意味着，假如人类的身体可以像橡胶人一样任意变形，那么用两手的拇指和食指做成两个套着的圆环之后，我们可以不放开手指，把圆环给解开来。 Algorithmic and Computer Methods for Three-Manifolds 一书里画了一张非常漂亮的示意图：

      

 
    更加有趣的是，如果仅仅是手腕上多了一块手表，上述方案就不能得逞了：

      

 
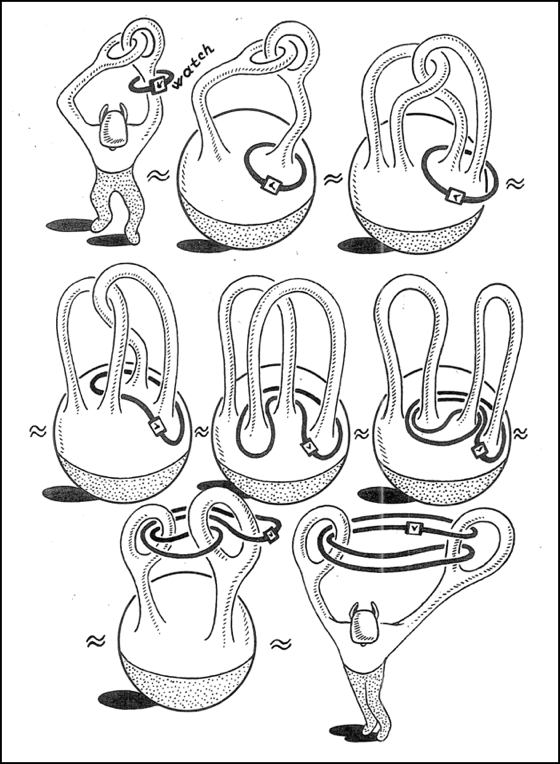
    2. 能否把左图连续地变为右图？

      

 
    答案是可以的，如下图所示：

      

 
    3. 左图所示的立体图形表面画有一个圆。能否通过连续变换，把这个圆变到右图所示的位置？

      

 
    答案是可以的，如下图所示：

      

 
    4. 在一个轮胎的表面上打一个洞。能否通过连续变换，把这个轮胎的内表面翻到外面来？

      

 
    答案是可以的。首先，作出如下图所示的连续变换。可以看到，一个表面有洞的轮胎本质上等于两个粘在一起的纸圈！不过，注意纸圈 1 和纸圈 2 的地位不太一样：一个是白色的面（即最初轮胎的内表面）冲外，一个是阴影面（即最初轮胎的外表面）冲外。现在，把纸圈 2 当成原来的纸圈 1 ，把纸圈 1 当成原来的纸圈 2 ，倒着把它们变回轮胎形，轮胎的内外表面也就颠倒过来了。

      

 
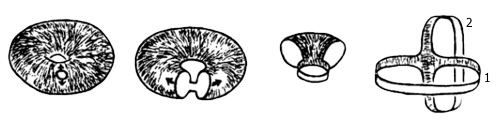
    有趣的是，把轮胎的内表面翻出来之后，轮胎上的“经线”和“纬线”（姑且这么叫吧）也将会颠倒过来：

      

 
    Wikipedia 上有一个巨帅无比的动画，直接展示出了把一个圆环面的内表面翻到外面来的过程。此动画看着非常上瘾，小心一看就是 10 分钟！

      

 
    5. 能否把左图连续地变为右图？

      

 
    答案是可以的。首先，作出如下图所示的连续变换，于是就变成了问题 1 中的图 (a) 。再利用问题 1 的办法，即可变出我们想要的形状来。

      

69 条评论

发表评论




Enter Captcha Here :