经典证明：Ptolemy定理的无字证明

    Ptolemy 定理是平面几何中非常漂亮的定理：圆内接四边形的对边乘积之和等于对角线的乘积。具体地说，如果把一个圆内接四边形的四条边顺次记为 a 、 b 、 c 、 d ，把两条对角线的长度记为 e 和 f ，那么一定有 a · c + b · d = e · f 。 Ptolemy 是一个非常重要的定理，由它出发可以得出很多推论。例如，在圆内接矩形上应用 Ptolemy 定理，可以立即得到勾股定理。下面是另外两个可以用 Ptolemy 定理来解决的问题：证明余弦定理，以及构造两两间的距离都是整数的点集。

     William Derrick 和 James Hirstein 在最近的 The College Mathematics Journal 上给出了下面这个 Ptolemy 定理的无字证明，你能看明白吗？

      


 
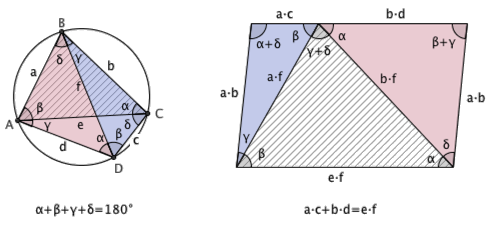
    左图是一个圆内接四边形，由于同弧所对的圆周角相等，因而图中会产生四对相等的角，我们用 α 、 β 、 γ 、 δ 来标记。由于圆内接四边形对角互补，因此有 α + β + γ + δ = 180° 。现在，把阴影三角形放大到原来的 f 倍，这个三角形的三边将会变为 a · f 、 b · f 、 e · f 。把红色三角形放大到原来的 b 倍，于是三条边的长度将会变为 b · a 、 b · d 、 b · f 。注意到两个放大后的三角形都有一条长为 b · f 的边。同样地，把蓝色三角形放大 a 倍，三边长将变为 a · b 、 a · c 、 a · f ，它和放大版的阴影三角形都有一条长度为 a · f 边。因此，我们可以像右图那样，把三个放大版的三角形拼到一起。由于 α + β + γ + δ = 180° ，因此右图中上面那三个点是共线的，整个图形是一个四边形。观察四边形四个内角的关系可以很快看出，这个四边形是一个平行四边形。因而，它的上下两条对边应该相等，于是有 a · c + b · d = e · f 。

 
来源：http://www.cut-the-knot.org/proofs/PtolemyTheoremPWW.shtml

31 条评论

发表评论

47  +    =  57