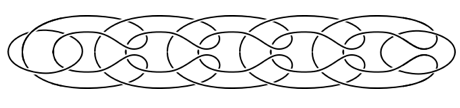
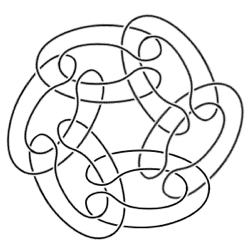
下图中的三个绳圈套在一起，没有哪一个绳圈能从中分离出来。不过，真正有趣的是，如果去掉其中任意一个绳圈，那么其他所有的绳圈都全部散开了。如果 n 个绳圈套在一起，并且任意去掉其中一个绳圈都会同时解开其他所有套着的绳圈，我们就把它叫做 n-component Brunnian link 。
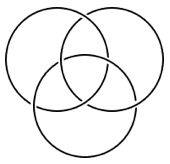
你能想出一个 n = 4 的 Brunnian link 吗？ n = 5 呢？ n 可以任意大吗？
Wikipedia 上给出了一个 n = 4 的 Brunnian link ，如下图所示：
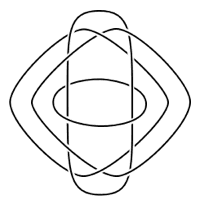
这个网页中给出了两种方案，据此可以得到任意大的 n-component Brunnian link ：
杀花
拓扑学······嗯大牛好久没更新了啊······
第一反應是九連環……
哈哈。有意思。
曾在《绳圈的数学》中见过，但下面这几个太牛了
不錯不錯很漂亮！！！！！
还有一种办法，如果你经常用橡皮筋/细绳栓钥匙环的话。就是把一头套进去然后折回来从另一头伸出来，拉紧。这种也是可以做成两头用环封闭或循环结构的，大概想了下应该跟上边的图是不等价的。
阅过，终于盼来一篇文章
Hello大家好，我是J. V. King
我也要一楼
不懂，n的时候的第一个图，最左边的线切掉，后面能拿下来么？
环不能是刚体，否则套不上、、、、
想到某些解环类的连环玩具……
环状那个真给力啊，话说如何能够提高对绳圈的空间想象能力呢？看了半天……
赞
九连环
都说是绳圈了那就否定了刚体。9连环是不是呢？是那就得松松跨跨的。
感觉3连环和wiki的图想起来很复杂啊。如果绳子是软的是不是可以把wiki的图修正成类似后两个图那样。只考虑交点不考虑环的形状。
九连环
看了几篇楼主的博客，顿时发现自己智商低了不少啊！跟不上楼主的节奏…不过也发现了数学有这么多有趣的东西…
在现实中，可以用n个绳套套餐这些形状吗？
是套成
越看越觉得自己智商低了不少啊！跟不上楼主的节奏…不过也发现了数学有这么多有趣的东西…
看来你的插图，我确定我找对地方了。
看了你的“人生、杯具”的图，很喜欢这种线条的风格~
楼层: 21楼 | 2012-11-27 23:13 | 乌江踏月 说：
在现实中，可以用n个绳套套餐这些形状吗？
＝＝＝＝＝＝＝＝
可以。取一纸带，将纸带扭曲360度后用胶水把两端粘在一起。（莫比乌斯圈是扭转180度。）沿纸带面中间剪开成n个环，即得n元Brunnian link。如果非要用绳子，可类比这一过程只不过粘结改为打结。
我帖错地方了，请忽略我上面的言语。我提到的方法只能得到任意一个绳结皆与其他绳结相套而已。无法实现任意去掉其中一个绳圈都会同时解开其他所有套着的绳圈。汗颜汗颜
话说我小时候买来的橡皮筋就是这么连的，我老是拿它连绳子玩，用的时候，拆一个下来，别的就都散了。。。
Rolfsen的Knots and links里给除了另一种办法……不过不知道评论怎么贴图，只好贴在链接里了。
其实n环的第一种让我想到了丝瓜巾。。。就是洗澡用的，长条的，一环扣一环的那种，确实是打开了一个就都散了。。。