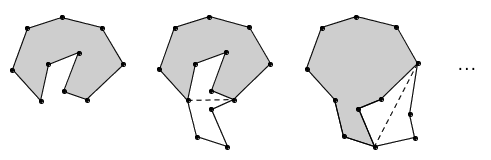
左图是一个凹多边形，而且凹得相当厉害。作为一个完美主义者，我很难容忍这么一个图形，总想着要把凹进去的部分翻出来，把它还原为一个凸多边形。不幸的是，翻折之后的结果仍然不是凸多边形，图中又产生了新的凹陷。于是，我们想继续把凹进去的部分往外翻，直到整个图形变成凸多边形为止。问题是，这个过程有完吗？换句话说，我们一定能通过有限多步翻折，把凹多边形变成凸的吗？
这个问题有着非常纠结复杂的历史。这个问题最早可能是由数学家 Paul Erdős 正式提出的。 1935 年，他在 American Mathematical Monthly 上猜想，经过有限步翻折之后，凹多边形一定能变凸。 1939 年， Béla Szőkefalvi-Nagy 给出了一个证明。因此，这个结论又叫做 Erdős-Nagy 定理。有趣的是，这个问题是如此的自然，以至于在此之后，又有一大堆人重新提出并研究了这个问题，而且他们明显并不知道相互之间的已有研究。这事儿给我们带来的好处就是，我们有了 Erdős-Nagy 定理的好几种截然不同的证明方法。不过，这些证明或者太长，或者太高深，或者又有些漏洞。 1999 年， Godfried Toussaint 从这些证明中取长补短，给出了一个比较初等的证明。
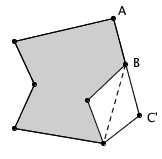
在下面的讨论中，我们可能会遇到上图所示的情况：某次翻折之后，三个相邻顶点正好共线，构成了一整条长边。那么，今后中间的那个点将永远位于这条边上，因此我们可以放心地把它从顶点集里去掉。于是，我们可以默认，下面讨论的所有多边形，边上都不会有“废”的顶点。
让我们先来看一个引理：任意给定一个凸多边形后，我们总能找到一个 ε ，使得只要该凸多边形的每一个顶点都移动了不超过 ε 的距离，得到的新多边形仍然是凸的。
让我们考虑凸多边形上的某个顶点 Vi ，以及它的两个相邻顶点 Vi-1 和 Vi+1 。把 Vi-1Vi 的中点和 ViVi+1 的中点的连线记为 l 。于是， Vi 、 Vi-1 、 Vi+1 这三个顶点到 l 的距离都是相等的。让我们把这个距离值为 r 。现在，以 r 为半径，分别以这三个顶点为圆心作圆，那么，只要每个顶点都在各自的圆内移动，这些顶点与直线 l 的相对位置都保持不变， Vi-1 和 Vi+1 仍然在 l 的同侧， Vi 仍然在 l 的另一侧。也就是说，整个多边形在 Vi 这个点仍然是凸的。注意到，对于每个不同的顶点 Vi ，我们都能找到这么一个合适的 r 。取所有这些 r 当中的最小值，它就是一个满足要求的 ε 。
下面我们开始证明，对于任意的一个凹多边形，经过有限次的翻折后，最后总能变成一个凸多边形。
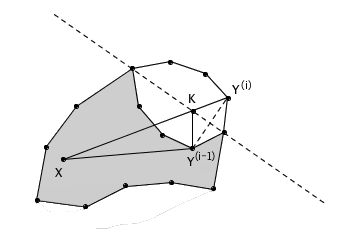
首先，让我们考虑初始时多边形内的任意一点 X ，以及多边形上的任意一个顶点 Y 。今后，这个 Y 点的位置将不时发生变化。我们把第 i 次翻折之后 Y 点的位置记作 Y(i) 。注意到，由于每次翻折之后，新的凸多边形都完全覆盖了原来的凸多边形，因此 X 将永远留在凸多边形的内部。现在我们来考虑每一次翻折对 X 和 Y 之间的距离将带来怎样的影响，在第 i 次翻折之前， X 和 Y(i-1) 都在翻折的折痕同侧，在第 i 次翻折之后， Y 点要么根本没动，要么被对称地翻折到了折痕的另一侧。在前一种情况下， X 到 Y 的距离并没有变；在后一种情况下，假设 X 和 Y(i) 的连线与折痕交于点 K ，则 XY(i) = XK + KY(i) = XK + KY(i-1) > XY(i-1) ，可见 X 到 Y 的距离严格地增加了。
但是，多边形的翻折操作不会改变整个多边形的周长，因此 X 到 Y 的距离有一个上限：它最多等于整个多边形周长的一半（类似于上图的极端情况）。这表明， XY(1), XY(2), XY(3) … 的长度构成了一个有上界的不下降序列，因而这个序列有一个极限。也就是说，最终 Y 点到 X 点的距离会慢慢固定下来。注意到，由于 X 的任意性，因而我们实际上说明了，随着翻折次数的增加， Y 点到初始多边形内的任意一点的距离都会固定下来，因此事实上， Y 点存在一个极限位置。根据同样的道理，多边形的所有顶点都将慢慢趋近于它们各自的极限位置，因此整个多边形也就存在一个极限。显然，这个极限多边形一定是凸的，否则它还能再翻折，与它是一个极限相矛盾。
别忘了我们之前的引理：我们总能够找到一个 ε ，使得极限多边形的每个顶点都移动不超过 ε 的距离之后仍然能保持凸性。现在，在极限多边形的每个顶点周围都画上一个半径为 ε 的圆盘。对于初始多边形的每一个顶点，它最终都会收敛到它的极限位置，因而在有限步翻折之后，它必然会踏入它所对应的圆盘。因此，我们只需要等待有限步翻折，所有的点都会踏入各自的圆盘。此时，我们便得到了一个凸多边形。
这个证明很有意思：结论本身是离散的，证明却用到了连续和极限的思想。由此带来的结果是，我们虽然证明了凹多边形能在有限步之内变凸，但却完全无法给出所需步骤数的一个上限，哪怕是一个很松很粗略的上限！
沙发？
周长固定
面积小于同周长圆
每次翻折增加面积大于0
暂时想到这点
话说没有刻度，只有表面和3根相同或不同的针的表能读出时间么
3根针重叠好像只有12点，其他能读出时间的角度还有不
我考虑过这样一个问题但没想明白：任意一个正星多边形是否都能通过有限次翻转变成相应的正多边形呢？
又见Matrix67发帖，我订阅你的blog应该有两年了，我有个问题，跟这个主题没关系，跟你的几何图有关系。我一般都用PPT来画这些东西，但是只能做到差不多，不能做到精确，我这几天想画一张尺寸精确的图，发现PPT很难做到，即使我把PPT的grid打开。我知道CAD工具可以，但是那也太复杂了，而且如果我想把公式放在图上，也没法做到，我想问问你blog上的这些图是用啥画的？
如果只用距离或者面积的话只能说明存在一个极限多边形但不能证明只需有限步即可变成凸多边形，前面的引理巧妙地解决了这个问题，太神奇了
“显然，这个极限多边形一定是凸的，否则它还能再翻折，与它是一个极限相矛盾。”
为什么是极限就不能再翻折？
感觉这个思路是先想的证明主体再想的引理……
原文花了一些篇幅来address这个问题，在：
http://cgm.cs.mcgill.ca/~godfried/publications/erdos.pdf
学校有ScienceDirect订阅的可以看：
http://www.sciencedirect.com/science/article/pii/S0925772104001373
原来如此
直接看题目感觉应该证一下对于某一图形翻折增加面积有大于0的下界什么的
地下室见FAQ，我也问过这问题，貌似还不止一遍。。
are you god?
沒有討論走進循環的情形(可能根本就不會有循環, 但總得討論下吧)
@Kaa1el 不会有循环的，因为 X 和 Y 的距离在每一次翻折之后是严格增大或不变的。
我认为到了“这个极限多边形一定是凸的，否则它还能再翻折，与它是一个极限相矛盾。”就已经结束了，引理里的圆盘的作用是在证明什么呢？
与pseudo prime 同感，求解
“注意到，由于每次翻折之后，新的凸多边形都完全覆盖了原来的凸多边形，因此 X 将永远留在凸多边形的内部。”
其中的“凸多边形”应该是“凹多边形”吧。
@12a与14： “这个极限多边形一定是凸的，否则它还能再翻折，与它是一个极限相矛盾。”这个地方不能算结束，到这里为止只是证明了极限的存在，但是极限存在不等于极限可在有限步骤内达到，而需要证明的命题是“有限步”，因此最终需要借助这个引理来完成这个“有限步”的约束。
@12楼：那个距离严格递增的论述就已经彻底排除了循环的可能。
感觉这个证明有些问题：一是没有证明不同翻折顺序能得到相同的极限多边形；二是并没有证明在到达极限之前就已经是凸多边形，而引理是关于凸多边形的，因此实际上用不上
@18楼
第一，证明本身不依赖于“不同翻折顺序能得到相同的极限多边形”，只需要在任意一个翻转操作序列下存在极限就可以了，而不同的翻转序列对应的极限可以不一样，不影响证明。
第二，你没看懂最后一段的含义。
最后一段跳跃性是有点大，我来尝试解释一下：这一段的核心是极限的概念。按照极限的概念定义，一个序列有极限，不代表这个序列可以在有限项之后达到这个极限值。因此如果不包括最后一段，整个证明是不成立的。但是同样从极限的定义方式可以得到一个推论：对于一个存在极限的序列，任意给定一个接近于极限值L的值a，一定存在一个确定的N，使得序列中从第N项开始，每一项和极限值L之间的差都小于a与极限值L之间的差。特别要注意到这个N是确定的值，是有限的。
那么在前面的过程中，已经证明了极限多边形存在，并且这个极限多边形是凸的。我们单独考虑某个顶点Y，不妨假设在极限多边形中Y所对应的顶点为Y’，每一次翻转，我们都把Y’与Y的距离d记录下来，这样就形成了一个序列：d1,d2,d3,…… 这个序列的极限为0。那么现在我们给出定值ε，这是一个大于0的值，根据极限的定义，那么一定在这个序列中存在一个N，使得dN开始每一项都小于ε。也就是说，N步之后，这个顶点就会落入那个圆盘之中，并且在这以后也不会再跳出圆盘。考虑所有的顶点，分别考虑对应的N值，取其中最大的那个，不妨称为Nmax，根据上面的论述，可知经过Nmax步（有限步）之后，所有的顶点都落入了对应的圆盘之中。再利用一下引理，就可以知道在这个时刻，所有顶点所连起来的多边形必定是凸的。也就是说我们已经一个有限值Nmax，在经过Nmax步操作之后，多边形已经变成凸的了。这就是我们想要证明的命题。
再多嘴几句：首先呢，对于不同的操作序列，对应的Nmax值可能是不同的，并且Nmax步之后，所形成的凸多边形也可能是不同的，但是命题本身不要求相同，因此这不构成证明的漏洞。第二呢，命题对于“翻折”这个操作的描述还不够严谨，最重要的就是要排除翻折三个共线相邻顶点的可能，也就是说必须保证每次翻折之后，多边形的面积严格增加。否则的话不停地翻共线顶点，就永远结束不了了。
这篇好难看懂，但是直觉告诉我肯定可以翻成凸多边形
有个问题，每一次翻出来的区域有限制么？还是随便找一个凹的区域翻出来都行？如果这样的话，像这样的图：
http://goo.gl/MjkQp
翻出来后多边形内的点X和顶点Y的距离不就变近了么？
再利用一下引理，就可以知道在这个时刻，所有顶点所连起来的多边形必定是凸的//这是有问题的，引理的前提是一个无退化顶点的凸多边形，每个顶点在ε邻域内移动时不改变凸性。而且，如果极限多边形是凸的，如果含有退化顶点（即相邻三顶点共线时中间那个顶点就是退化顶点），则顶点在ε邻域内移动时凸性不能保持，原证明中排除退化情形的方式也不严谨。
除了引理被以循环论证方式运用外，极限多边形的存在的证明也不严格，虽然这个容易补救：到给定点的距离存在极限，并不直接表明点列收敛到ε圆盘内。补救方式是证明到给定的三个点的距离都存在极限。而且，给出一个唯一确定的翻折顺序是严谨论证的一部分。
这个证明貌似缺少了一个环节,并非对于任何X和任何Y以及任何折法,XY长度都会增大,因为存在一些情况使得折后的Y和X位于折痕的同侧(比如最开始的图片如果第一步是折叠内部中心位置靠左上角的那个钝角,而X点取在图形的右下角)
所以应该对折法有所限制,只允许对整个多边形在其一侧的折痕进行操作,所以还要证明永远存在这样的合法操作
还是描述上的问题，对于“翻转操作”需要有一个更加严谨的描述，25楼的补充是必须的，即每次翻转所使用的对称轴不能穿过图形内部。在这个需求下，出现退化的顶点就可以排除出去，不再影响引理。
我还是认为“废顶点”的处理有问题。极限多边形中的废顶点，并未被证明会在有限次翻折后形成。那么证明中的这段话“某次翻折之后，三个相邻顶点正好共线，构成了一整条长边。那么，今后中间的那个点将永远位于这条边上，因此我们可以放心地把它从顶点集里去掉”就不成立，而极限多边形有废顶点的话，所有证明都不严谨了。
“在第 i 次翻折之前， X 和 Y^(i-1) 都在翻折的折痕同侧”
nice~这样想就合理了～
翻折后y到x的距离逐渐逼近极大值能说明y的空间位置也收敛到极限吗？ 或许它可以不断跳出那个epsilon的小圆？
感觉XY距离不递增啊。。这个需要修正。。
@27 极限多边形是我不断操作得到的，既然我每次操作中会排除掉所有废顶点，那么极限多边形肯定也不存在废定点
@30 既然我每次操作中会排除掉所有废顶点，那么极限多边形肯定也不存在废定点//仍然不严谨。你假定了废顶点一定会在有用顶点到达极限点之前先废掉，这是需要证明的，否则完全可能在有用顶点（即极限多边形中的真凸顶点）到达极限位置之后才废掉。
用面积单增且有上界可以么？
终于想到一个自认为满意的证明。
定义一个顶点的内角和外角中较小者为该顶点的“劣角”。
［引理一］任意顶点的劣角在翻折中单调不减。
证明：显然，一个顶点在翻折中如果不是“桥墩”（即位于翻折轴上）则劣角不变，只需证明桥墩的劣角不减即可。
翻折轴和一个桥墩形成K形局部图形，K形的竖线即为翻折轴，不失一般性假定被翻转的边是K形的“撇”。
令K形朝上的角为a>0，朝下的角为b>=0，显然，翻转前劣角为180-(a+b)，则翻转后劣角为180-|a-b| >= 180-(a+b)。
证毕。
根据引理一，每个顶点的劣角在翻折中构成单调不减序列，这个单调序列上界是180度，因此极限存在。
定义劣角极限为180度的顶点为“退化顶点”，否则为“非退化顶点”。
定义一个顶点和它的两个相邻顶点决定的三角形为“贴身三角形”。
一个顶点被翻动时，凹顶点（即内角大于180度）变成凸顶点（即内角小于180度），凸顶点变成凹顶点。显然，凹顶点被翻动时，多边形增加的面积不小于该凹顶点贴身三角形的面积。
［引理二］非退化顶点不会无限次被翻动。
证明：因为非退化顶点P的每两次翻动，多边形面积至少增加P的贴身三角形面积；
而因为P是非退化顶点，劣角的极限<180，故其贴身三角形面积的极限大于零，因此无限次翻动P将导致多边形面积无限增加，与多边形周长恒定有限相矛盾。
证毕。
根据引理二，每个非退化顶点都将在有限次翻折之后不再被翻动，故存在一个最大的步数（即翻折次数）M，在M步完成时所有非退化顶点都到达了它的极限位置而不会再被翻动。
在M步完成时，任取退化顶点P，往正方向找出第一个非退化顶点X，往反方向找出第一个非退化顶点Y。由于M步之后X、Y将固定不动，因此连接XY并含有P的一组边X..P..Y的总长度的极限为|XY|（因为该组边的每个角的极限都是180度，即该组边的极限位置是一条直线段）。
由于X..P..Y总长度在翻折中保持不变，因此在M步后X..P..Y总长度应恒等于极限值|XY|，即M步后X..P..Y已经为直线段，亦即所有退化顶点都完成了退化，不再被翻动。
于是经过有限的M步，凹多边形被翻折成了凸多边形。证毕。
提一个有趣的新问题
如果边数n一定，则要翻折的次数是有限的。
比如说n=3时，三角形一定是凸的，所以翻折的上限是0；
当n=4时，容易证明四边形最多只要翻折2次，就成为凸四边形了。
定义记号B(n)：要让n边形要变成凸的，最多需翻折次数为B(n)。
那么对每个n，B(n)是不是有限呢？已B(3)=0，B(4)=2，那n>4时呢？
我认为到了“这个极限多边形一定是凸的，否则它还能再翻折，与它是一个极限相矛盾
B(5)=4?
回复12L：谢飞月同学，不可以。无穷靠近某个值的面积导不出矛盾
m67大牛，弱弱的问一句，是否存在正整数n，对任意的正整数M，即使边数为n的多边形无论怎么折都不会出现消顶点的情况，也可以让它需要翻折至少M次才可以变成凸的？
如果这个结论成立，那么这一定是一个神奇的n边形序列
如果不成立，那么，翻折次数是不是一个增长很快的函数？能干掉graham函数吗？能干掉燃绳函数吗？
今天又有点疑惑了。万一极限多边形有一条边是两条边拼起来的怎么办。。。
，不可能吧，函数又不是“连续”的，跳跃式连续，说不清楚，就是图像应该是单调上升的折线
周长固定，面积肯定有最大值，面积最大值时肯定是凸的，每次操作面积都在增加
What’s up, yup this article is really good and I have learned lot
of things from it about blogging. thanks.