Heron 公式是一个已知三角形三边长便能直接求出其面积的经典公式。把三角形的三边长分别记作 a 、 b 、 c ，令三角形的半周长 p = (a + b + c) / 2 ，则三角形的面积可以用 Heron 公式 S = √p(p – a)(p – b)(p – c) 求出。如果把 p = (a + b + c) / 2 代入式子，得到的公式其实也挺对称的： S = √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) / 4 。

    现在，我们把这个公式看作是一个关于 c 的函数： f(c) = √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) / 4 。它的导数是多少？

    注意到，利用平方差公式，根号内的式子可以进一步整理为 ((a + b)² – c²)(c² – (a – b)²) ，它的导数是 – 2c(c² – (a – b)²) + 2c((a + b)² – c²) = 4c(a² + b² – c²) 。因而，整个原函数的导数就是 c(a² + b² – c²) / (2 · √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) ) 。

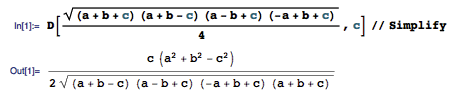
    有趣的是，当 a 、 b 、 c 满足勾股定理的关系 a² + b² = c² 时，导数值正好为 0 。这是为什么？ Heron 公式的导数的零点和勾股定理有什么联系呢？

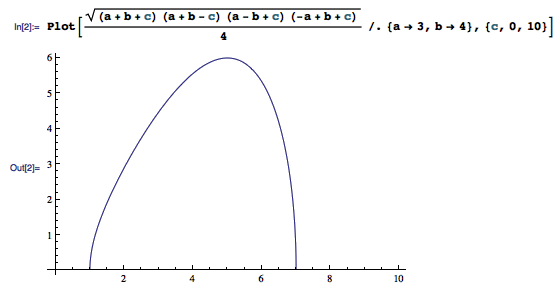
    假设一个三角形其中两边的长度已经固定，分别为 a 和 b 。但是，这个三角形的第三条边 c 是不确定的，因此整个三角形是活动的，三角形的面积也就成了一个关于 c 的函数 f(c) 。其中， c 的取值范围是从 |a – b| 到 a + b ，同时函数值从 0 开始逐渐增大，最后又变回 0 。而 f'(c) = 0 则给出了三角形面积达到极大时的情形。什么时候三角形的面积达到极大呢？

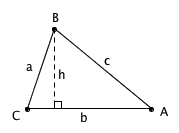
    如图，我们把 b 水平放置，并考虑 a 绕着它们的公共端点转动。显然，当 a 、 b 成直角时，三角形的高 h 最大，因而整个面积达到极大，此时 a² + b² = c² ，这正是 f'(c) = 0 的一个解。

    真正神奇的是，我们完全有可能用这种方法，反过来去证明勾股定理！与此有关的详细讨论，可以参见 http://www.cut-the-knot.org/pythagoras/HeronsDerivative.shtml