今天见到一种看上去很帅的质数筛选法。在平面直角坐标系上画出抛物线 y = x2 的图像，然后标出抛物线上的所有格点（两坐标均为整数的点）。其中，只有点 (0, 0) 正好在 y 轴上，其余的点要么在 y 轴左侧，要么在 y 轴右侧。把 y 轴左侧除了 (-1, 1) 以外的所有格点与 y 轴右侧除了 (1, 1) 以外的所有格点相连，这些连线将自动避开 y 轴上纵坐标为质数的点。连接足够多的线条之后，质数就逐渐露了出来。
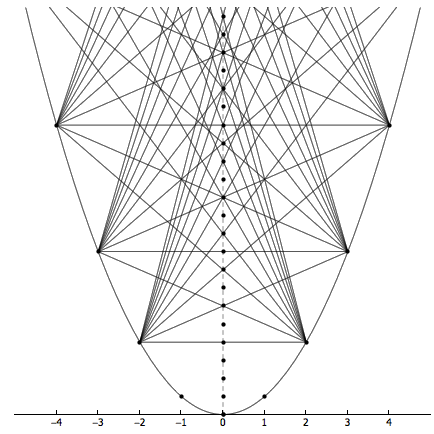
这是因为， (-a, a2) 和 (b, b2) 的连线将经过 (0, a · b) ，这可以通过计算斜率的方法得到验证。这个颇具创意的质数筛选法叫做 visual sieve ，它是由 Yuri Matiyasevich 和 Boris Stechkin 提出的。
查看更多：
http://plus.maths.org/content/catching-primes
http://www.mathteacherctk.com/blog/2011/10/the-parabolic-sieve-of-prime-numbers/
沙发..
太v5了
神奇！
天呐⋯⋯
总觉得……
M67的文质量在下降呢……
这图画出来得多巨型啊
很有想法，不错
帅！凭着构造这个不知能不能搞定什么猜想噢……想想……
我觉得你的水平应该可以自己研究一些东西了吧，哈哈，好想看你自己原创的对数学的奇妙思考和新奇方法。期待啊~
个人感觉这个还可以继续探究
赞个 挺神奇的 hoho
经过了斜率的推算(-a, a2) 和 (b, b2) 的连线将经过 (0, a · b)是和很明显的结论，作者的想象力很不错，但是在计算的时候还是会使用质数筛选法。这个方法就只能作为一个质数赛选法的可视化的解释了。
看似简单的结论算了半天。。
来试试头像啦
很有想法，不错
确实有趣
不交点的就是质数
很酷，但是不能简化算法
如果你认为金钱是万能的，很快就会发现自己陷入痛苦之中。