上一次写这玩意儿已经是两个月前的事了，今天突然想起这一系列的东西我还没有写完。和上次一样，我们将对另一个几何问题作出光学和力学两种解释。由于前面已经有了不少铺垫，很多东西这里就不再重复了。

  
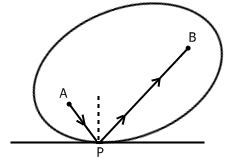
    椭圆是平面上到给定两点的距离之和为定值的点的集合。那两个定点就叫做椭圆的焦点。椭圆有一个神奇的性质：选定椭圆上的任意一点P，把它和两个焦点A、B相连，则PA和PB与椭圆在P点处的切线有相同的夹角。换句话说，PA和PB与法线的夹角相等，即入射角等于反射角。这样的话，任意一条从A出发的光线，经过椭圆壁的反射后总会经过另一个焦点B。假如有一个餐厅是椭圆形的，你的位置恰好位于椭圆的一个焦点上。这时你突然听到不知哪里传出的一男一女谈情说爱的声音，其肉麻程度不堪入耳，并且声音格外清晰。不用怕，这是因为那对男女正好坐在另一个焦点上，他们谈话的声音再小你也听得见，因为这些声音经过房间墙壁的反射后全汇聚到你这里来了。
    你可以用解析几何证明这一结论，不过其复杂程度令人望而生畏。这是我上学期做的最恶心的一道高数题。有趣的是，这个结论用Fermat原理（光总是沿着所花时间最短的路径传播）来解释的话，根本不需要运算，几句话就说清楚了。我们需要证明这样一个几何命题，椭圆上一点P与焦点A、B的连线到过P点的切线的夹角相等。把过P点的切线作出来后，我们可以一眼看出这个论断是正确的：从点A出发的光线经切线反射后过点B，则反射点一定就是点P，因为切线上所有其他的点P'都在椭圆外，折线A->P'->B都比A->P->B长。

  
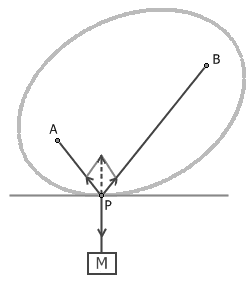
    后来，我在《数学与猜想》中看到了另外一种物理证明方法，非常神奇。这个结论的正确性可以通过一个非常简单的力学模型揭示出来。看上图，我们在两个焦点间连接一条长度为2a的绳子，绳子上挂一个重物。注意到重物是挂在绳子上的，绳结处P是可以活动的。显然，P点的轨迹形成了一个椭圆。重物有不断下落的趋势，此时重力势能转化为动能；当整个力学系统静止时，重力势能达到最小，因此最终绳结P应该位于椭圆的最低点，该点处的切线正好是一条水平线。此时绳结P受到了三个力：重物M所产生的垂直向下的力，以及左右两边的绳子的拉力。由于物体保持平衡，两个拉力的合力必须竖直向上才行。但绳子内部的张力处处相等，两个方向上的拉力大小应该一样；如果它们的合力竖直向上，那么这两个力的方向与竖直方向的夹角必然相同。于是我们得到了和上面的讨论相同的结论：椭圆上的点与两焦点的连线到法线的夹角相等。