几道经典的几何作图趣题

    这段时间的古代汉语课和现代文学史课的时间利用得很好，我已经看完了Mathematics and Plausible Reasoning Vol.II和How to Solve It，并且已经读完了What is Mathematics的第一章。前面两本书主要是对数学思维方法的系统研究，有趣的新鲜东西并不太多。书里拿了几道比较经典的几何作图问题当作例题，比较有意思，在这里与大家分享一下。

1. 顺次给出四条边a, b, c, d以及对边a与c的夹角α，作一个四边形；
2. 给你一个三角形，作出一个内接于此三角形的正方形（正方形的四个顶点都落在三角形的边上）；
3. 已知三角形的一个角α，这个角所对的边的高h，以及这个三角形的周长p。求作这个三角形。

  
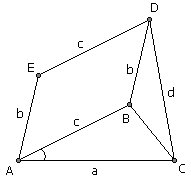
1. 顺次给出四条边a, b, c, d以及对边a与c的夹角α，作一个四边形：先作出△ABC，其中AC=a，AB=c，两边夹角为α。然后分别以b和d为半径，在B点和C点画弧相交于D。平移AB和BD补成一个平行四边形ABDE。四边形AEDC即为所求。

  
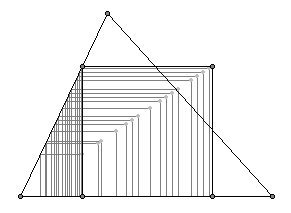
2. 给你一个三角形，作出一个内接于此三角形的正方形：不妨先尝试满足部分条件，只让三个点落在三角形的边上。可以证明第四个点的轨迹是一条直线，问题迎刃而解。

  
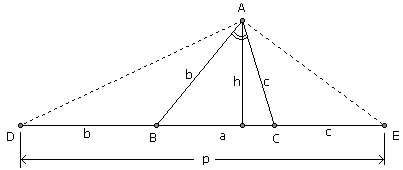
3. 已知三角形的一个角α，这个角所对的边的高h，以及这个三角形的周长p。求作这个三角形。这题有点难。你需要集中精力思考，那个周长应该怎么放才合适。于是想到用作等腰三角形的方法把三条边拼接到一条直线上去。这样问题转化为作一个底边为p，对角为α/2+90°，高为h的三角形。此三角形的顶点A由一条平行于DE的直线与一段圆弧的交点所确定。这段圆弧可以这样作：先随便作一个满足∠DA'E=α/2+90°的△A'DE，显然△A'DE的外接圆上与A'同侧的所有点对DE的张角均为α/2+90°，而这个外接圆的圆心就是A'D和A'E的垂直平分线的交点。找到△ADE后，AD和AE的垂直平分线与DE的交点即为点B和点C。

9 条评论

发表评论

2  ×    =  6