考虑这样一个双人对弈游戏：在一个8×8的方阵里分别填上1-64这64个正整数。然后A和B两个人轮流在格子中取数，A先取，B后取。取数的规则很简单：取过的数不能够再取，并且除了第一次以外，以后每次取的数必须与某个已经取过的格子相邻。所有数都取完后，所取数之和最大的人获胜。
    很显然，这个游戏对于A更有利一些。我们可以轻易构造一个初始状态，使得先取的人必胜。考虑A的这样一个策略：总是取能取的数中最大的一个。如果每次A都可以取走整个棋盘中最大的那个数，那A就赢定了（因为每次B接下来取的数都比A小）。这样的初始状态是很容易构造出来的，比如我们只需要从左往右从上至下依次填入这64个数就可以了，这可以保证如果从n到64的所有数都取走了，则n-1也可以被取走。
    现在的问题是，能否构造一个初始状态，使得后取的人有必胜策略？提示，解决这道题需要有超强的“整人”能力。你得想出足够多的坏点子才能找到弄死先行者的方法。你的心肠坏到足以解决这个问题吗？

  
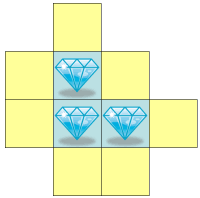
    解决问题的关键在于，我们要给A埋下“陷阱”。考虑这样一种局部构造：奇数个大数彼此相连，这些大数周围一圈全是小数。上图就是这样一个陷阱，钻石代表大数，其余黄色的格子都是小数。只要A踩进了某个黄色格子，他就中计了：B和A开始轮流取大数，但大数只有奇数个，因此B获得的大数比A多一个。为了让事情变得更简单，我们只考虑最简单的一种陷阱：只有一个大数，周围的邻格都是小数。我们还有几个难点：万一A一开始就把陷阱内的钻石取走咋办，又如何避免自己不会掉进陷阱，还有我们必须保证B从这些陷阱里赚到的足以弥补在其它地方亏的。要想有足够多的陷阱对A起作用，我们得布上至少三个陷阱，这样A可以在最能赚的陷阱里开局，但无法避免落入另外两个陷阱。为了保证自己不会掉进陷阱，我们可以把棋盘的其余部分划分为多米诺骨牌（一个个1×2的小长方形），这样的话不管A取哪一个格子，B总可以取对应的另一个格子，不会踩到陷阱。于是我们想到了下面的这个构造：

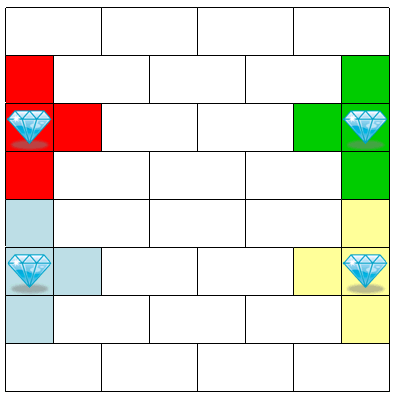
    我们在四个陷阱里分别填上1-2-3-61，4-5-6-62，7-8-9-63，10-11-12-64这四组数，每个多米诺骨牌里填上两个相邻的数。这样的话，A的最好策略就是从第一个陷阱里开始取数。他能从第一个陷阱里赚到(61+2)-(1+3)=59分，但他在其它陷阱里将分别丢掉(62+4)-(5+6)=55分、(63+7)-(8+9)=53分、(64+10)-(11+12)=51分。而多米诺骨牌一共只有24个，他最多只能捡24分回来，这是远远不够的。因此，先取者必输无疑。

参考资料：http://www.brand.site.co.il/riddles/200802q.html