今天听说了 Conway’s Soldiers ，这是 Conway 大牛在 1961 年提出的一个数学谜题（似乎 Conway 的出镜率也太高了），我觉得非常有意思，在这里跟大家介绍一下。内容基本上来自于 Wikipedia 的相关页面。
假设有一个无限大的棋盘。棋盘上可以放置一些象征着士兵的棋子。一个棋子可以跳过并吃掉和它相邻的一枚棋子（就像孔明棋一样）。这是棋子的唯一一种移动方式。现在，在某个位置画一条无限长的水平线，你需要在水平线下面放置足够多的棋子，使得它们前仆后继地往水平线上方跳，最终能够跳到水平线以上 n 个单位的位置。
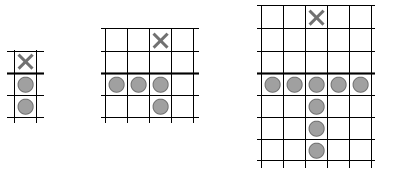
如图所示，当 n = 1 时，两个棋子就够了。当 n = 2 时，我们需要 4 个棋子。当 n = 3 时，最少需要 8 个棋子。
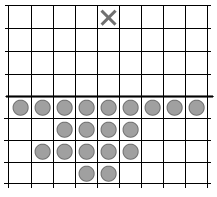
我们还能让士兵们冲到更远吗？可以的。下图显示的就是 n = 4 的最少棋子摆布方案，它一共要用 20 枚棋子（看看你能不能看出具体的移动步骤）。有趣的是， Conway 证明了下面这个或许有些不可思议的事实：当 n = 5 时，这个问题就不再有解了。换句话说，无论用多少个初始棋子，我们都不可能冲到 5 个单位远的位置去。这个证明过程非常神奇，它竟然和黄金分割莫名其妙地扯上了关系。
我们给每个格子标一个关于 x 的单项式。把目标格子标记为 x0 ，也就是 1 ；一个格子离目标格子有多少步（相当于 manhattan 距离），就给这个格子标上 x 的多少次方。于是，整个棋盘就变成了下面这样。棋盘上的若干棋子形成的布局，也就对应了一个关于 x 的多项式。例如，下图中的 6 枚棋子就对应了多项式 x4 + 3 · x5 + 2 · x6 。
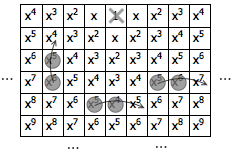
每次移动棋子，我们都会改变一个棋子的位置，同时从棋盘中拿掉另一个棋子，从而让整个多项式发生变化。我们把棋子的移动分成三类：正向移动、中性移动、背向移动（分别如上图中左、中、右三个棋子跳跃的例子）。所谓正向移动，也就是朝着目标点的方向跳跃，棋子落点处的指数比出发点的指数更小。假如棋子的出发点所在位置是 xn，那么这次跳跃给整个多项式带来的变化就是减去了一个 xn ，加上了一个 xn-2 ，并且还减去了一个 xn-1 。我们可以记作 xn-2 (1 – x – x2) 。中性移动就是指一个棋子从标有 xn 的格子跳到了另一个标有 xn 的格子，和目标点的距离并未变化，仅仅会让棋盘上少一个棋子 xn-1 。因此，这种移动给整个多项式带来的变化就是 – xn-1 。背向移动则是往远离目标点的方向跳跃，它给多项式带来的变化则是 – xn + xn+2 – xn+1 ，即 xn (x2 – x – 1) 。
现在，我们需要选取一个适当的底数 x ，使得正向移动给多项式带来的变化为 0 。为此，我们需要让 x 满足 1 – x – x2 = 0 ，解得 x = (±√5 – 1) / 2 。我们选取其中的正数解 (√5 – 1) / 2 。出人意料的是，它正是神奇的黄金分割数 φ ≈ 0.618 。
这样，棋盘的每个格子都对应了一个形如 φn 的正实数，其中目标点是 φ0 ，也就是 1 。定义一个棋局的价值为各个棋子位置上所对应的正实数之和。任何正向移动都不会改变布局的价值，其它形式的移动都会让价值变小。我们的目标就是把整个阵型的价值变成 1 （或者更大，如果最后还有残余棋子的话）。
注意 φ 的一些有趣的性质。由于 φ2 = 1 – φ ，不断在等式两边乘以 φ ，我们还可以得到 φ3 = φ – φ2 ，φ4 = φ2 – φ3 ， φ5 = φ3 – φ4 等等。把等式左边全部加起来，也就得到 φ2 + φ3 + φ4 + … = 1 了。
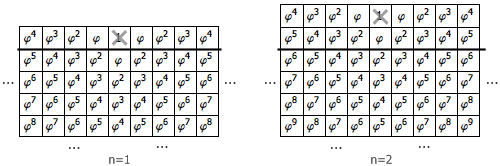
当 n 等于 1 时，水平线以下第一行的格子的价值总和是 φ + 2 · φ2 + 2 · φ3 + 2 · φ4 + … ，第二行每个格子的价值分别是第一行对应格子的 φ 倍，第三行格子的价值则再乘以 φ ，以此类推。因此，水平线以下的所有格子的总价值为：
(φ + 2 · φ2 + 2 · φ3 + 2 · φ4 + …) (1 + φ + φ2 + φ3 + …)
= (φ + 2)(1 + φ + 1)
= (φ + 2)2
= φ2 + 4 φ + 4
= 5 + 3 φ ，
其中，最后一步再次用到了 φ2 = 1 – φ 。
当 n = 2 时，水平线离目标点的距离增加一个单位，从而导致每个格子的价值都乘以了一个 φ ，于是水平线下的所有格子的价值总和就是 (5 + 3 φ) φ = 5 φ + 3 φ2 = 3 + 2 φ 。类似的， n = 3 时水平线下方的格子总价值为 (3 + 2 φ) φ = 3 φ + 2 φ2 = 2 + φ ， n = 4 时这个值变为了 (2 + φ) φ = 2 φ + φ2 = 1 + φ ， n = 5 时这个值变为了 (1+ φ) φ = φ + φ2 = 1 。这表明，当 n 等于 5 时，如果在水平线以下的所有格子里都放上棋子，总价值正好为 1 。当然，棋子的数量不可能是无限的，因而初始布局的价值是严格小于 1 的，我们不可能把它变为一个价值大于等于 1 的棋局。这就说明， n = 5 时问题是没有解的。
貌似沙发？
板凳
搶個位子xd
膜拜。
1、对于楼主“今天”才知道此题我比较惊奇，因为《稳操胜券》下册就有。
2、小说《深夜小狗神秘事件》用到了这个谜题。
看了你的回复才知道还有《深夜小狗神秘事件》这么个小说 刚刚读到这个谜题那里 还是个不错的小说。《稳操胜券》是本什么书呢？
以前看到过，不过名字叫做“五星上将”，就是每向上超过横线一个单位就是获得一颗星。这个游戏充分说明了“一将成名万骨枯”的道理……
唔。。。
“ 现在，我们需要选取一个适当的底数 x ，使得正向移动给多项式带来的变化为 0 。”
为什么？
为了确保守恒啊
数学无力中。。。
这种问题居然还能用多项式求解……屌爆了……
Conway特别喜欢这种……类似细胞机的游戏嘛
太牛了！！！把实际问题转化成数学问题，通过一个简单的多项式就证明了实际中不可能用实验来完成的问题。太酷了！！！
最多多长？
shift4已出，请速写介绍。
原来如此！
哇靠，数学真的是万能的啊，这思维。。
厉害呀佩服呀
是呀，为什么呢？
我们需要选取一个适当的底数 x ，使得正向移动给多项式带来的变化为 0
回16楼：选取一个适当的底数 x ，使得正向移动给多项式带来的变化为 0，这样做有两个好处：一、任何正向移动都不会改变布局的价值，其它形式的移动都会让价值变小。（这样就限定了布局的价值一开始就必须大于等于1）二、φ2 = 1 – φ ，也才有φ2 + φ3 + φ4 + … = 1（这样可以比较方便地求出布局的价值）。但第一个才是这么做的主要原因。
如果n>5呢？
更准确地说，应该改成“当>=5时，这个问题就不再有解了。”
这问题在两本书里面看过，一本名字忘记了，还有一本是台湾的《科学月刊》
我自己还试着推导过一次，可以证明对于赋予任何值的格子都不可能，不一定要用黄金分割。
设目标格子的值为（x0），离目标格子距离n步的格子的值为xn，且对于任何n有xn=xn-1+xn-2
考虑第二行后面所有格子的值：
(1)x2+3*x3+5*x4+7*x5+…
上式=(x2+x3)+2*(x3+x4)+3*(x4+x5)+4*(x5+x6)+…
=x1+2*x2+3*x3+4*x4+…(2)
(2)-(1)=x1+x2-x4-2*x5-3*x6-…=x0-(x4+2*x5+3*x6+…)=x0-((x5+x6)+2*(x6+x7)+3*(x7+x8)+…)
=x0-(x5+3*x6+5*x7+…)
被减数是目标格子的值，减数是第五行之后所有格子的值，因为（2）式等于（1）式，所以差为0，x0=(x5+3*x6+5*x7+…)，证毕。
此外，有没有有没有适用于无穷多棋子情况的解？（就像无穷囚犯问题http://www.matrix67.com/blog/archives/444那样）
1+3*x
谁是conway，Damian Conway？
回20楼：应该是John Conway，就是研究细胞自动机的那位
用无穷多步把棋子走到第五格的方法太神了……
有些复杂。。
不愧是Conway。。。
博主，x值的不同怎样体现棋盘的棋子布局和个数？
是个关于必要条件的证明吧，必要条件不成立，原命题（n>=5 有解）当然不成立。。。
证明很经典啊。。。。
不过话说，n<5时怎么找出解的啊？别告诉我是暴力的。。。。
从19L得到的灵感，其实我们要证明x5+3×6+7×7+9×8+…<=1
然后Xn=Xn+2 + Xn+1
这样：
x5+3×6+5×7+7×9+…
=(x5+x6)+2(x6+x7)+3(x7+x8)+4(x8+x9)+…
=x4+2×5+3×6+4×7+…
=(x2-x3)+2(x3-x4)+3(x4-x5)+4(x5-x6)+…
=x2+x3+x4+x5+x6+…
=(x0-x1)+(x1-x2)+(x2-x3)+(x3-x4)+(x4-x5)+…
=x0
=1
Q.E.D.
这样对不对？
回23L，n=1,2,3,4时可以用逆推法来办，就是想办法形成n-1时的状态，只是往前一格而已。
纯粹前来实验头像。。。
Great hammer of Thor, that is poflwruely helpful!
92年用作了IMO国家队的选拔试题
当年我好像是在一个日文网站上看到这道题的，还用象棋子摆了半天
精彩，本来想问问题的，但是想明白了
这解法。。。牛爆了
19L的差分方程确实是更一般的，其通解其实就是黄金分割的幂的线性组合。
Conway的证明只取了其中一个黄金分割的幂，这样可以降低证明的复杂度，反正证伪只需要有一个反例就够了。
太牛了！！！把实际问题转化成数学问题，通过一个简单的多项式就证明了实际中不可能用实验来完成的问题。太酷了！！！
我是在搜索您的一篇文章时来到这里的。我记得您曾写过一篇关于斐波那契数列与黄金分割数的文章，里面还有动态演示的图片，但是我现在找不到了，能告诉我在哪吗？
Hello there! propecia best online pharmacy discount best online pharmacy
5个棋子在初始有无限枚棋子时是可以达到的