最难的组合游戏：To Knot or Not to Knot

    A Midsummer Knot’s Dream 简直可以说是去年学术界的一篇奇文，大家点进去看看就知道了。论文里讲了一个基于纽结理论的双人对弈游戏，名字也非常有艺术感： To Knot or Not to Knot 。这个游戏可能是最难的组合游戏了，它的数学性极强，思考难度非常大，甚至比 ERGO 更不容易上手。一场游戏下来，究竟谁赢谁输可能都不好判断。

    To Knot or Not to Knot 的游戏规则非常简单。用铅笔在纸上画一个封闭的、可以自相交的回路，然后 A 、 B 两人轮流在图形中选取一个尚未被处理过的交叉点，并用橡皮擦对图形进行“细化”，明确两根线条的位置关系（可以抛掷硬币决定谁先行动）。A 的目的是要让最终的图形变成一个结，而 B 的目的则是避免图形打结。下面是其中一种可能的游戏过程，双方约定 B 先走。两人轮流对交叉点进行细化，七步之后，整个图形并未打结（你能看出来吗）， B 获得胜利。

      

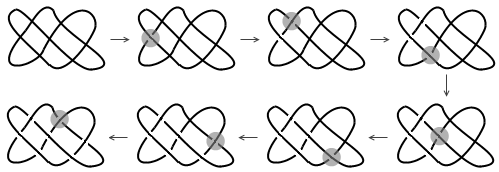
    注意，这是一个决策透明、信息公开的游戏，并且游戏不可能有平局产生。因此，即使双方都使出最佳策略，也必然有一个人会赢有一个人会输。也就是说，任意给定一个初始状态，总有一方有必胜的策略。不过，难就难在，究竟谁有必胜策略，必胜策略是什么，这并不容易判断。让我们来做一个练习题吧：下面的图形中，如果 A 先走，B 后走，谁有必胜策略？如果 B 先走，A 后走呢？记住，A 的任务是要让最终的图形打成结，而 B 的任务则是避免图形打结。

      


 
 
 
 
 
 
 
 
 
 
 
 
 
 
      

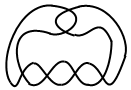
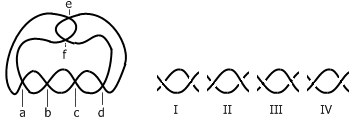
    答案是，两种情况下，后走的人都是必胜的。为了便于叙述，我们用 a 、 b 、 c 、 d 、 e 、 f 来标记图中的六个交叉点。对于两根线条连续两次相交的地方，最终只可能是右图所示的 I 、 II 、 III 、 IV 四种情形之一。我们把前两种情形叫做“假交叉”，把后两种情形叫做“真交叉”。

    注意到，如果 B 能把 (e, f) 变成假交叉，那么不管下面四个交叉点是什么样，整个图形必然不打结。因此，如果 B 是后走的，那么 B 一定可以获胜：一旦 A 动了 e 、 f 中的一个交叉点，那么 B 立即细化另一个交叉点，让它成为假交叉；否则， B 就陪着 A 在下面四个交叉点中玩。但是，下面只有四个交叉点，是一个偶数，因而最终 A 将被迫对 e 或者 f 进行细化，从而宣告 B 的胜利。

 
      

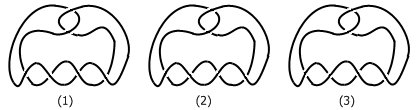
    如果 A 是后走的人呢？ A 也将必胜。 A 可以把六个交叉点分成 (a, b) 、 (c, d) 、 (e, f) 三组，然后 B 细化了哪一个交叉点， A 也就跟着修改同组的另一个交叉点，从而决定每组交叉点的交叉类型。 A 可以把 (e, f) 变成真交叉，把 (a, b) 和 (c, d) 当中的一个也变成真交叉，另一个变成假交叉，这便能保证让整个图形打结（如图 1）。需要注意的是，把下面两组交叉变成一真一假，这是必需的。如果下面两组都是假交叉，得到的图形仍然没有打结（如图 2）；而如果下面两组都是真交叉的话，最终的图形也不见得就一定是一个结（如图 3）。

 
    有没有什么图形能够让先走者必胜，不管先走者是谁呢？当然有。我们只需要把刚才的图形中任意一处线条扭一下，得到的新图形就满足要求了。先走的人就先把这里进行细化，整个图形就退化成了原来的图，先走的人此时也就成为了后行者，便能套用刚才的必胜策略了。

      

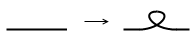
    当然，也存在这样的初始局面，使得必胜者并不是由先行后行直接决定的，还要具体看先行者是谁后行者是谁。这里就不再举例了。有没有什么更有意思的初始局面？判断必胜方有什么简便方法吗？能否迅速找出必胜策略呢？似乎目前都还没有什么漂亮的答案。

33 条评论

发表评论




Enter Captcha Here :