生成函数的妙用：平均抛掷多少次硬币才会出现连续两个正面？

    在一篇老日志中，我提到了一个经典的概率问题：平均需要抛掷多少次硬币，才会首次出现连续两个正面？它的答案是 6 次。它的计算方法大致如下。

    首先，让我们来考虑这样一个问题： k 枚硬币摆成一排，其中每一枚硬币都可正可反；如果里面没有相邻的正面，则一共有多少种可能的情况？这可以用递推的思想来解决。不妨用 f(k) 来表示摆放 k 枚硬币的方案数。我们可以把这些方案分成两类：最后一枚硬币是反面，或者最后一枚硬币是正面。如果是前一种情形，则我们只需要看前 k – 1 枚硬币有多少摆法就可以了；如果是后一种情形，那么倒数第二枚硬币必须是反面，因而这种情形下的方案数就取决于前 k – 2 枚硬币的摆放方案数。因此我们得到， f(k) = f(k – 1) + f(k – 2) 。由于摆放一枚硬币有两种方案，摆放两枚硬币有三种方案，因而事实上 f(k) 就等于 Fk+2 ，其中 Fi 表示 Fibonacci 数列 1, 1, 2, 3, 5, 8, …的第 i 项。

    而“抛掷第 k 次才出现连续两个正面”的意思就是，最后三枚硬币是反、正、正，并且前面 k – 3 枚硬币中正面都不相邻。因此，在所有 2k 种可能的硬币正反序列中，只有 Fk-1 个是满足要求的。也就是说，我们有 F1 / 4 的概率在第二次抛币就得到了连续两个正面，有 F2 / 8 的概率在第三次得到连续两个正面，有 F3 / 16 的概率在第四次得到连续两个正面⋯⋯因此，我们要求的期望值就等于：

     


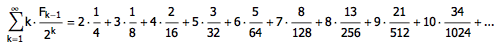
    这个无穷级数就等于 6：

      

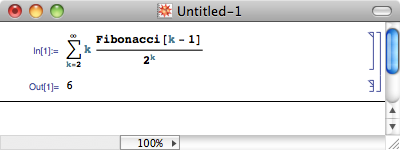
    不过，最后这一步来得也太假了，因为我们借助了强大的 Mathematica 。今天重新翻到这篇旧日志时，我就在想，究竟怎样求出这个无穷级数呢？这个数列的某些特征让我联想到了生成函数这一数学工具，用生成函数处理这样的数列非常合适。我在很早很早以前就写过介绍生成函数的文章，但遗憾的是，我对生成函数运用的了解，仅仅局限于教材和网络上给出的各种经典例子，从没有亲自用到过生成函数。今天算是我第一次真正使用生成函数，深感生成函数之妙。如果你是第一次看到生成函数的应用，想必你会大吃一惊，这种诡异的方法竟然能把答案搞出来！整个过程用到了很多生成函数的经典处理手段，这让它足以打败教材上的各种经典例子，成为了我最爱的生成函数应用例题之一。

 
 
    让我们先来说说什么是生成函数吧。生成函数就是对数列进行编码的一种方式。我们可以用一个含有无限多项的多项式（注：这个说法是不准确的，有无限多项的不能叫多项式） a1 · x1 + a2 · x2 + a3 · x3 + … 把整个数列的全部信息装进去，其中第 i 次项系数就表示数列的第 i 项。因此，Fibonacci 数列的生成函数就可以写成：

     

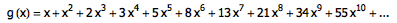
    厉害就厉害在，我们可以把生成函数表示成一个更简单的形式。先来看看 g(x)·x 的结果：

     

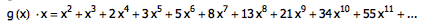
    再看看 g(x) + g(x)·x 的结果：

     

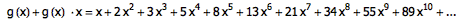
    你会发现， Fibonacci 数列的递推性质，使得上面这行式子与 g(x) 本身非常相像。事实上，如果把 g(x) 的每一项都除以 x ，再减去最前面多出来的 1 ，就能得到上面的这行式子了。因此，我们有：

     

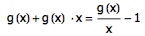
    我们甚至可以就此解出 g(x) 来：

     

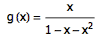
    于是，整个无穷级数 g(x) 被我们化简为了一个关于 x 的代数式！注意，虽然这个等式只在 x 充分小（小到级数 g(x) 收敛）的时候才有意义，不过这并不妨碍我们用这个代数式来代表 Fibonacci 数列的生成函数。我们可以把 Fibonacci 数列看作是生成函数的一个“展开”：

     

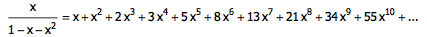
    也就是说，这么一个小小的代数式就容纳了 Fibonacci 数列的全部信息！

 
 
    生成函数是如此地具有代表性，以至于在研究数列时，我们常常会给出它的生成函数。在数列百科全书 OEIS 中，生成函数几乎是必不可少的一项。例如，在 Fibonacci 数列 的描述中，FORMULA 一栏的第一行就是 G.f.: x/(1-x-x^2) ，说的就是 Fibonacci 数列的生成函数（generating function）。

    更绝的是，我们还可以直接对数列的生成函数进行变换，从而得到新的数列。比方说，在生成函数上再乘以一个 x ，我们就会让每一项的 x 的指数加 1 ，从而让整个数列右移一位，得到了一个新的数列 Fi-1，即 0, 1, 1, 2, 3, 5, …

     

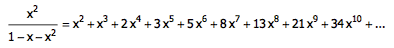
    现在，我们需要用各种代数运算手段，对等式左边的生成函数进行变换，让等式右边的展开式变成本文开头的那个数列。什么操作能够同时让数列第 1 项除以 2 ，第 2 项除以 4 ，第 3 项除以 8 ，以此类推，让所有的第 i 项都除以 2i 呢？我们可以把所有的 x 都用 x / 2 来替代：

     

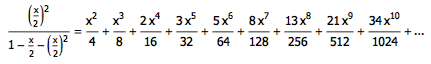
    化简一下：

     

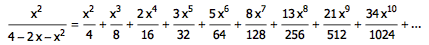
    这就是数列 Fi-1 / 2i 的生成函数了。接下来，我们想要让第 i 项系数乘以一个 i ，也就是想要让每一项的系数都乘以该项的次数，这该怎么办呢？最神奇的地方出现了——我们对生成函数进行求导：

     

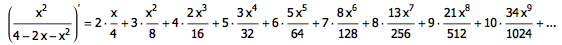
    也就是：

     

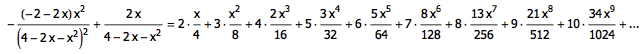
    不过，求导的同时，x 的次数也移动了一位。我们在生成函数上再乘以 x ，把 x 的次数纠正回来：

     

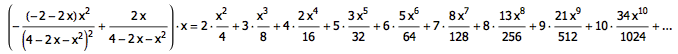
    这就是本文最初的那个数列的生成函数了。令 x = 1 ，便有：

     

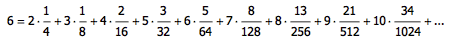
    Tada！

44 条评论

发表评论




Enter Captcha Here :