这道题的答案有几个字母？答案：four。
有趣的是，这是唯一的答案。如果令函数 f(n) 表示非负整数 n 的英文表达中有多少个字母（不算空格和短横线）， n=4 是该函数的唯一不动点。
n 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
f(n) 4, 3, 3, 5, 4, 4, 3, 5, 5, 4, 3, …
事实上， @IanMathmogician 发现了一个更有趣的“数学冷知识”：任取一个 0 到 100 之间的整数 n ，算出这个数的英文表达中的字符个数，再算出所得结果的英文表达的字符数，并这样一直迭代下去，最后总会得到数字 4 。我用 Mathematica 做了一张图片，可以让大家直观地看到，这真的可以说是条条大路通向数字 4 啊。
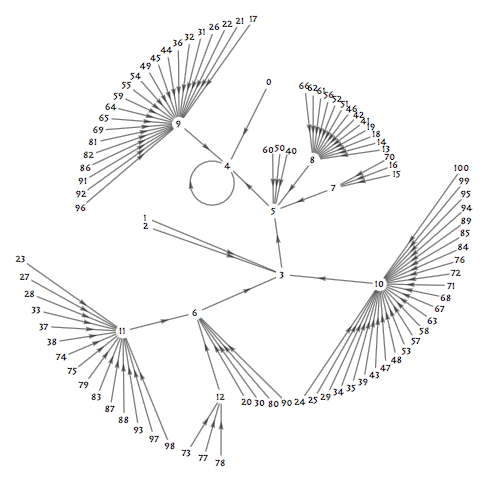
那么，对于更大的数，如此迭代下去也都会变成 4 吗？恐怕没有人会置疑这一点吧。事实上，由于数字的英文描述所需字符数是对数级别增长的，因此从理论上说，对于更大的数，英文表达所用的字符数都应该比这个数字本身更小。于是，反复取字符数，所得结果必会越来越小；到了充分小的时候，就会按照上图的指示掉进数字黑洞 4 里。
我另外画了一张从 0 到 1000 的所有数的转移示意图，非常壮观，贴在下面供大家观赏。
查看更多：http://www.reddit.com/r/math/comments/jarub/interesting_mathematical_curiosity/
沙发?
好久不见更新了啊~这个图确实壮观。
挺有意思的，还有好玩儿的东西么？
诡异的图片
很有意思
这个会不会是一个大反例
这个会不会是一个大反例
这个会不会是一个大反例…..?
这图真酷，不知道Mathematica怎么画出这种图的！
请问Matrix67你拿Mathematica的Graph作图的那些参数设置是什么
弄了半天没成功把点变成数字，把箭头变好看点
中文数字就不一样了。有一、二、三三个不动点，然后四和五相互循环
一个比较容易想到的扩展是把英文表达的字符数换成中文表达的笔画数，又可分为简体和繁体。举个简单的例子，一、二、三肯定是不动点，四、五相互振荡。可能统计笔画数没有统计字符数那么方便
在文字中寻找规律，特别像一些数列，在高数中学过，趋势趋于一个定值，lim值存在
matthen也是个mathemarica的爱好者啊
数学就是真善美啊！
1000那个图好帅……
Mathematica怎么画这种图的。。
图真漂亮
真有趣。
matrix67, 你快去读数学系吧。别再耽搁了。
数学好神奇~
f(n)=n就是最后的终结数，而4符合。
觉得应该是巧合吧
真的好壮观
看图前在想，是因为所有字符数最终还是会回归1-10，而这10个数的字符数也就分别是3，4，5，最终3→5→4. 然后看到图，发现图解释的清晰多了=_=.
这怎么看不懂？
这个知识夸张了，实际上刚好four是4个字符。所以到four这死循环了。如果英文four造字是for.3个字符，还有上面的图吗？
夸张了。实际上刚好英文four为4个字符，到这死循环了。如造字时4的英文为for,还有上面这图吗？
数字组成线条，线条组成图片。好棒好棒
@legend
如果这样的话，应该会有个3→5→4→3的环吧。。