我老早就写过一个经典的小学几何题。如果你还没看过这个问题，你一定要去看看。一个小学奥数老师曾经告诉我，当年带领学生参加这次竞赛时，领队老师们都没有想到这个问题的“小学生解法”，以至于开始质疑这道题是否超纲了。看到答案后，老师们大为折服——这个问题确实有一个无需任何几何知识的妙解。
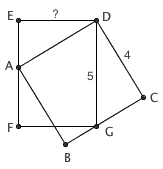
今天，同样的事情发生了。今天临时去代一节小学奥数课，见到这么一道题： ABCD 是一个正方形，边长为 4 ， DEFG 是一个矩形，其中 DG = 5 ，求 DE 的长度。还是那段话：题目本身并不难，大家一看就知道答案；问题的关键在于，这个问题是一道小学竞赛题，这意味着这个题目一定有一个异常巧妙的傻瓜解。这个解法不用相似形，不用列方程，事实上几乎什么都不用，只需要用到最基本最显然的正方形长方形的性质。你能想到这个解法吗？
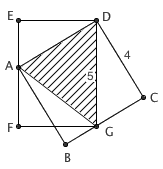
我叫了几个初中数学老师来，一起围着它研究了半天，结果想破脑袋也还是满脑子的相似，于是只好求助小学组的老师，果然取得真经，赞不绝口，大呼妙哉。连接 AG ，注意到三角形 ADG 的面积既是正方形 ABCD 面积的一半，又是矩形 DEFG 面积的一半，可见正方形和矩形的面积是相等的。既然正方形的面积是 16，矩形的一边长是 5，另一边就是 3.2 了。
你想到了吗？
我晕……我还在那边想着割补法……
mark!!!
sf?
前些时代小学奥数课去了…今天有空啊
很神奇啊。不小心翻过头一下子看到答案的图了。瞬间懂了。
小学奥数什么的最厉害了。。。当时学小学奥数的时候老师就说过有些题大学生都不会~
超赞！
这。。。无话可说。。。我还在想勾股定理呢。。。
小学的时候肯定做得出来的TUT。。。
我才初二，小学奥数还没有忘光啊，想了一会就看出来了。嘻。
先占个楼，话说我也在想着怎么割补呢，偶然翻了一下tyvj，发现原来在vijos上的‘文科生的悲哀’又出现了。。
http://begin.tyvj.cn:8080/Problem_Show.asp?id=1054
话说我是先用相似和方程解出了EG=16/5，然后思路应该是从正方形和长方形面积相等来做，然后开始按照这个思路来证明的面积相等。。。
同感 同感。。。
我把那个矩形看成由正方形构造的，G点在BC边滑动，可形成一系列矩形，两个极端图形分别是正方形本身，和一个面积与正方形相同的矩形，于是猜测题中矩形面积与正方形相等。我试着证明：正方形面积和矩形相等。过A点作DG的垂线可以证明。只不过，最终我的证明还是用到了相似。
说来圆也有个类似的……
虽然猜到要往面积相等方向证，不过5,4,3太有迷惑性了，一直在想这是不是勾股定理的一种证法
我是小学老师，一下就想到了，是不是小学老师的思维就定势如此呢
原来如此。。。
这个解法很赞！
另一个解法是相似三角形，标着5和4的三角形和要求边长的三角形一看就是相似的。
4 * 4/5 = 3.2
看到5，4条件反射地想到3，然后就想不到面积的事了。。。
我怎么一看到就想到了勾股 = =
呵呵，想到是这样，却说不出两者面积相等的理由
呃…..想了5分钟才想到。要是没有强烈暗示，肯定还是照相似的方法解题
小学做过
伤不起呀！想破脑袋每出来
呵呵，一开始就觉得这两块面积相等，一连接AG，就整出来了
看来小学教育就是比中学教育要赞……
其实作辅助线这种方法很多小学生应该也没有掌握吧？我印象里初中才接触。虽然你可以说这个方法不用教，可以悟出来，但这个悟出来的能力谈何容易。
想到了，嘻嘻。。。
谢谢楼主
看完答案,貌似想起小学好像做过这样的题…
这个题目真是又可爱又熟悉啊！
想到了，很典型的面积法啊
真是太喜欢你的博客了。。。。
那一章就没学好过…
张景中的一本小册子里遍地面积法
脑筋急转弯啊
这个题 相似形确实不难, 我也连出那条线了噢亲~三角形属于两个矩形面积的一半~哈哈
我给懵了~~汗，看了好久 了！
忍着不看答案，最终还是想到了……辅助线啊辅助线
我喜欢这类型的问题，楼主很强大。
还是那句话学好数理化，天下都不怕！学数学真益脑啊
想到了……
严重怀疑我的智商了。。。。。
我小学奥数基本没认真听，都是拿方程解的，惭愧……
事实上我们的初中数学教育主要教的是欧氏几何，而小学数学教育由于更加注重开发思路有些解法甚至于超越了欧氏的体系。等积法虽然看起来初级，连小学都有教，但其实它绝不简单。我的初中数学老师曾经跟我们提到过，中国有一位很牛的数学家曾经写过一部著作，他抛开了欧氏的体系，以等积、补形等拓扑方法为根本解决各种各样的几何问题，并且建立了一个初等几何学体系，而小学奥数有许多思路都是取材于他的著作。不过说实话，我已经离开初中六年了，他说的意思我到底有没有记清我也不算确定。
的確一看就知道答案是16/5了，
但是我是依據三角函數概念= =
额，我也想到相似去了。。
蒙了
高啊 我都晕
太牛叉了
难得自己想出来一道题~看来我小学数奥果然不是白学的~
想到了
话说用相似怎么证？
一眼没看出来
额，设AB交FG于Q，延长CB，EF交于P，则
S(DCG)+S(BQG)=S(APB)+S(BQG)=S(ADE)+S(AFQ)
则正方形和矩形面积相等……好吧，不算巧妙
奥数题的乐趣在于一题多解，让大家想出不同的解法是很让人惊喜的事情
呢滴个神丫……
开始想着旋转向量呢还……
小学时这样的题弄过不少，刚才看着想了1分钟就想到了，囧
我竟然隐约猜到了面积相等，然后得到了答案。
呵呵 我懂得怎么做了
还是忍不住看答案了, 忘了变成小学生后能用啥了, 呵呵
我小学的时候做过！！
延长EF 和BC 。。然后用平行四边形 来算面积。。。 小学奥数全是这种题
我小学肯定会，现在不会了。。。
上述方法不是最简单的，大家再想想别的思路
其实好好求解就可以解答了
刚开始用勾股定理推算去了，算了一半，想起来相似形，发现DE/4=4/5.看了答案，不得不惊叹。。
最简单的思路：
DG×DE／2＝S△ADG＝AD×DC／2
高端的脑筋急转弯。
伤不起呀！想破脑袋每出来
好吧 满脑子都是相似~~~ 我要多看看小学奥数书了 挨~~~~~
晕
千里眼 我那表弟，一次来我家，他妈让我检查他的作文， 我发现了这样的一段： 今天是周末，我来姐姐家里玩儿， 从窗户往下看，我看到花坛里的小蚂蚱一蹦一跳的，可高兴了。。 我这个不淡定啊！！我家在4楼！！ 夫妻俩测试儿子将来的从业意向， 在客厅放了四样东西：书 （科学家）、钞票（经商）、 美女照 （好色）、茅台酒 （嗜酒），隐门后窥视。 儿子放学回家，环顾四周，确认无人后，将钞票夹入书本， 揣上美人照，拎起酒瓶，若无其事地进入自己的房间。 夫妇惊叹：MLGB，这孩子将来要从政。 一直倒到热水不停的溢出来我都没有松手。 和尚说： 哎，你怎么不一样？薛蛮子一烫就放手了。 我说： 茶杯贵。 戴了帽子我就认不出你来 话说包子上次被面条海扁一顿后，心情抑郁。 因此找了小龙包、菜包、水煎包、汤包等包一起去吃火锅去去霉气。 一进门看到了金针菇，包族不分青红皂白把金针菇打了一顿， 留下一句话说： 不要以为你戴了帽子我就认不出你来! 厕所太难找 一款哥开着宝马在街上兜风，见前面急急走来一漂亮MM， 忙施展泡妞绝招：先狂按喇叭，见引不起她注意。 然后拿出一叠百元大钞顶在指尖上旋转，MM仍旧无动于衷。 情急之下，他拿出一箱金银珠宝在那儿显摆，结果MM反而加快了脚走， 边走边说： 这个城市的大款可真多，就是厕所太难找！ 升级了新版手机QQ 一大早心理诊所来了一位MM，从她红肿疲惫眼睛可以看出已经哭了一夜。 进门就开始哭诉男朋友如何冷落她，一夜QQ在线却一直不理她。 一定是变心，一定是有别人了，她感觉生命失去意义。 医生忍不住感叹爱情带给人几近疯狂的力量和执着。 良久，医生轻轻的问她： 你是不是升级了新版手机QQ？ 没素质乱扔手榴弹 小哈外出郊游买了瓶很逼真的手榴弹饮料。 喝完饮料后小哈就顺手把瓶子扔了出去。 只见一人提着裤子从草丛中跑了出来大骂道： 谁他妈这么没素质乱扔手榴弹呀？ 害的老子吓的连屎都没拉出来。 为了通知我们车都不要啦 阿明的车开到桥上突然没油了，便和朋友下来一起推车。 下坡时车直往下冲，阿明和朋友在后面挥手大喊： 车、车、车。。。 路边一卖水果的老奶奶拎起篮子拔腿就跑。 旁边人问她跑啥，她急忙说： 没听见人家喊撤吗？ 估计城管来啦、真是好人呀，为了通知我们车都不要啦！ 一哥们捡到后回了个1，我顺手给回复了个2。 没想法他马上又回了个3，我心想:好吧看谁更无聊！ 于是我回4他回5我回6他回7 就这样一直持续着。 当我回到782的时候实在顶不住，抱着手机就睡着了。 第二天醒了一看，那哥们自己从783数到了1000。 最后还给我留了句话：咱们明晚接着数。接着数。。。吃货比较单纯
我想到的方法是将整个图形看做是悬挂在墙上的画，D点看做是固定结构的钉子，旋转正方形，使得线段AD和线段DE平行重合。
最后得到一个式子4（4-ED）=ED*（5-4）=ED
ED=16/5=3（1/5）=3.2
Mark!!这也让我回想起了初中做平面几何时候常常被辅助线的作法给难住的日子了。
问题是，这没有实际意义。谁规定解题一定“不能”用某种超纲方法？戴着脚镣跳舞。如果某学生用超纲方法解出来，某老师说你超纲了，判解题错误，我只能说着老师是个SB。