经典证明：Cantor集中的元素两两相加可以遍历[0,2]

    今天看到一个有趣的证明，来源在这里。

      

    Cantor 集是一个简单而又神奇的分形图形。把 [0, 1] 三等分，挖去中间那一段（即挖去 (1/3, 2/3) ），然后把剩下两段也都分别进行三等分，并挖去各自中间的一段。这样无限地进行下去，最后得到的极限点集就是 Cantor 集了（上面那张图不是分割线，是 Cantor 集的一个示意图）。我们通常把 Cantor 集记作 C 。Cantor 集具有很多神奇的性质：它的 Lebesgue 测度为 0，但它却包含有不可数个点；它里面的每个点都不是孤点，但它却又是无处稠密的。你可以在这里看到一些具体的分析。

    Cantor 集还有很多其他的性质。若 A 、 B 是两个集合，定义 A + B = {a + b | a ∈ A 并且 b ∈ B} ，也就是 A 中的某个元素与 B 中的某个元素相加可能得到的所有结果。下面我们将证明，C + C = [0, 2]。


    下面是一个直观而又漂亮的证明。我们在平面直角坐标系上构造出点集 C × C，原问题就可以等价于，对于任意一个实数 a ∈ [0, 2] ，直线 x + y = a 都将经过这个平面点集中的至少一个点。

      

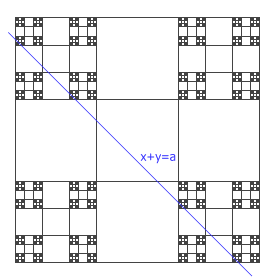
    注意到， C × C 也可以用下面的这个方法来构造。先把 [0, 1] × [0, 1] 分成九个小正方形，挖去中间的五个小正方形，剩下四个小正方形。注意到直线 x + y = a 是一条 45 度倾斜的直线，它不管摆在哪儿都会穿过至少一个角上的小正方形。我们继续对每个剩下的小正方形做“分割 – 擦除”操作，让每个小正方形也只剩下四个角。刚才那条直线也就会穿过它所经过的那个小正方形的其中一个角。如此进行下去，我们将会得到单位正方形的其中一角的其中一角的其中一角的其中一角⋯⋯最后就会收敛到一个点。这个点显然既属于直线 x + y = a ，又属于平面点集 C × C 。因此，只要 0 ≤ a ≤ 2，在 C 中总有两个数，他们的和恰好是 a。

29 条评论

发表评论




Enter Captcha Here :