2008-02-13 2:00| 
11 Comments | 本文内容遵从 
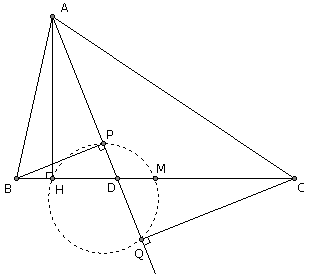
任意给定一个三角形ABC。令M为BC上的中点，令H为BC上的垂足。角A的平分线与BC交于点D。过B、C分别向角平分线AD作垂线，垂足分别为P、Q。证明H、P、M、Q四点共圆。
证明过程不复杂，几句话就说完了。但如果你能独立想出证明过程来的话也不简单。继续看下去前不妨先试试看。
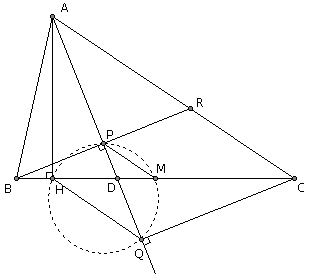
结论看起来似乎很神奇，但证明过程却并没有什么很特别的地方。
为了说明四点共圆，我们下面说明圆周角∠HQP=∠HMP。首先我们证明，∠HQP=∠ACB。由于∠AHC=∠AQC=90°，因此A、H、Q、C四点共圆，于是圆周角∠HQP=∠ACB。然后我们证明，∠ACB=∠HMP。延长BP后你会发现，P是BR的中点（AP既是角平分线又是垂线，等腰三角形三线合一），而M是BC的中点，于是PM∥RC，当然就有∠ACB=∠HMP。
题目来源：http://www.cut-the-knot.org/Curriculum/Geometry/BalticDarij1.shtml
平面几何真好玩啊……怀念一下初中的美好时光。
11 条回复
您也随便说几句吧：
Sofa.
Stool~~~~[razz]
Floor[music]
Ground floor
射影几何更好玩。
某些经典定理用常规方法需要证一页纸，用射影几何的方法两句话就完了，给人一种“你作弊！”的感觉。
回复：嗯，之前有接触过，过段时间打算开始系统研究射影几何
顺便问一下，你目前用什么软件画这类图形？我都用GeoGebra。
回复：几何画板
-.- 差点看成九点圆了...
数学一直一窍不通偏偏分数很高的人路过
回复：我恰恰相反，数学兴趣浓厚，偏偏考试分数巨低
呵呵，我给出另一种证法:
首先∠QHM=∠QAC=∠BAC=∠PHD
设过P，H，Q的圆和BC交于M'
所以有PM'==M'Q
延长PM'交QC于S
有PM'==M'S
有BPM'相似于CSM'
所以有BM'==CM'
所以M'就是BC的中点
我也来。
取AC中点E，连EM交AD于Q'，则有∠MQ'A=∠BAQ'=∠DAC，故有AE=EQ'(=EC)，得∠AQ'C=90°，即Q'和Q重合，所以∠MQA=∠BAQ=∠PHD，得证。
谁有做2010全国数学竟赛的12题