给定 n 个村庄的位置，要想把他们全部连通，最少需要修建多长的公路？这个问题被称为 Steiner 问题，是由数学家 Jakob Steiner 提出来的。注意，和最小生成树不同的是，公路是可以在中间汇合、分岔的。目前已经知道，Steiner 问题是 NP-hard 的，在规模很大的情况下，不能有效地得出最优解来。
然而，大自然却是无敌的，它可以迅速秒杀这样的难题。由于肥皂膜总会试图让自己的表面积最小，利用肥皂膜实验，我们可以轻易获得 Steiner 问题的解。我在很多书上都看到过肥皂膜实验的方法，不过却从没见过真正的实验视频。今天我终于看到了这样的视频，把它搬进墙来，和大家分享。这个视频也很好地解释了一个普遍存在的误区：说肥皂膜实验一举解决了 NP 问题是不恰当的，因为这个实验只能找到极小值，并不能找到最小值，运气不好的话，实验结果会是失败的。
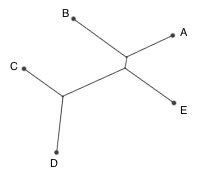
用物理方法解决数学问题，还有一个经典的例子：广义 Fermat 点问题。虽然实验的视觉感官可能没有那么振奋人心，不过还是召唤一下实验党吧。
SF
《什么是数学》里有的….
视频男很有激情啊
视频男说得不对，U型并不是Steiner问题的local minimum。至于肥皂泡为什么会停留在一个非local minimum上，我觉得是因为重力的原因，因为重力的干扰使得U型是张力的一个极值点。
在排除重力的情况下，肥皂液膜张力的极值点才等于Steiner问题里的极值点。
同darkraven:看到<>里确实有的.
同darkraven:<>里确实有的
那销魂的一吹
正N边形中肥皂膜形成的图样有些分形的意思啊
哦哦太有意思了
@地板，U型应该是local min，potential算上重力+张力的local min，重力对比张力太小，构不成perturbation吧
@地板，U型应该是把重力potential和张力potential一起考虑的一个local min……重力相比张力那么小算不上perturbation吧
牛B
这个哥们很有活力呀！
太给力了。
激情啊
8边形应该少一条边。
這個貌似一般寫作 Steiner Minimum Tree (SMT) 問題。用 MST 和 greedy 都能得到還行的 approximation ratio。
这不都是科技馆里逗小孩的东西么……点多起来之后这种解法也没什么意义……
日本有个科学小组，把食物点按日本城市的位置排放到培养皿里，然后观察某菌的生长状况，最后发现这种细菌到达各个点位置是最佳路径。
所谓的最佳路径好像指建地铁的最佳路径
有没有人觉得他小像Sheldon……
进行一次量子肥皂泡实验
从水槽里提起一个包含所有极小解（其中当然也有最小解）的叠加态
视频男说错了，U型的情况绝对不是极小值
如果是极小值那么应当是稳定平衡，但U型的情况受到某一方向的微小扰动就会偏离，因此它是不稳定平衡，应当是拐点或区间极大值（而且拐点的可能性更大，因为另一个方向的扰动不能使它偏离这个状态）
讲解的蛮不错的
god dame it’s cool! Thanks for sharing
u shape can be treated as a local optimal. It is like u formulate the objective of minimizing the length and use a gradient based method to search. but when u go to the terminal points do not have derivative. therefore it’s a trap as a “potential” candidate of “optimal”.
支持 支持
极小曲面也是这样啊……
Physics itself is computation.
恩恩，不错的解释
正六边形的肯定搞错了，连接任五边就行，其值为5，如果是视频中的那样就是3sqrt3约为5.169，大于5，当然不是最短
正八边形的，连接任7边值为7，如果是视频中的那样算一下约为8.009