上帝创造了整数，其余的则是我们人类的事了。正因为如此，质数、完全数、Fibonacci 数之类的数列才会让数学家们如痴如醉，因为它们的存在是如此自然，没有任何人造的因素。事实上，数学家们对这些数的认识也越来越丰富，挖掘出了这些数列中越来越深刻的性质。
不过，人类确实太渺小了。还有好多构造异常简单的“纯天然数列”，我们了解得实在太少。Kolakoski 数列就是最好的例子之一。
Kolakoski 数列仅由 1 和 2 构成，其中头 100 个数是
1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1,
2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1,
1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2,
1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2,
2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, …
如果我们把连续的相同数看作一组的话，整个数列的定义就只有两句话： a(1) = 1 ， a(n) 表示第 n 组数的长度。例如，a(6) = 2，就表明第 6 组数（从第 8 个数算起）的长度就是 2。注意，有了这几个条件，整个序列就已经唯一地确定了！a(1) = 1 就表明第一组数只有一个数，因此下一个数必须要换成 2 ，因此 a(2) = 2 ；而 a(2) = 2 又说明这个 2 必须要连着出现两个，因此 a(3) = 2；而 a(3) = 2 就表明数列接下来要有两个 1 ，等等。也就是说，生成这个数列的“参数”就是这个数列本身。更酷的说法则是，这个数列是分形的：如果把每一组数用它的长度来替换，就会得到这个数列本身。另外一个可能有些出人意料的事实是：Kolakoski 数列在 OEIS 中的序号非常靠前—— A000002。
关于 Kolakoski 数列，我们知道些什么？很少。我们知道，这个数列可以用递归式 a(a(1) + a(2) + … + a(k)) = (3 + (-1)k)/2 来表达。我们目前已经知道，去掉数列最前面的 1，剩下的部分可以从 22 开始，由替换规则 22→2211，21→221，12→211，11→21 迭代产生。
Kolakoski 数列的第 n 项有非递归的公式吗？目前我们还不知道。已经出现过的数字串今后都还会再次出现吗？目前我们也不知道。还有，我们有理由猜想，数列中 1 和 2 的个数各占一半。下图显示的就是数列前 n 项中数字 1 所占的比例，可见我们的猜想很可能是对的。
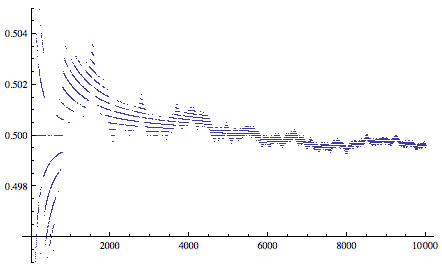
不过，目前还没有人能够证明这一点。而最近的一些研究则表明，数字 1 的比例很可能不是 1/2 。当然，还有第三种可能——这个极限可能根本不存在。这无疑又是一个最折磨人的数学未解之谜。
沙发……难得啊
沙发……怎么评论不上呢？
数学也有很多未解之谜
这个数列真强。数学真神奇。
希望发更多的神奇数学
第一次见此数列，第一次这么靠前
博主博客不错，星尔来支持下，欢迎回访。(*^__^*) 嘻嘻
太神奇了
义务劳动，给出Mathematica代码。
a = {1, 2, 2};
For[n = 3, Length[a] < 100, n++,
a = Nest[Append[#, 2 – Mod[n, 2]] &, a, a[[n]]]];
a
稀有数列……
謝謝地幔.summerdawn
果真是惊奇数学事实啊！支持博主
a(3) = 2；而 a(3) = 2 就表明数列接下来要有两个 1 是什么意思?
看懂了
因此下一个数必须要换成 2 ，因此 a(2) = 2
这里为啥a(a)=2 ?
我试了一下，计算到a(50000)，1出现的概率在25000时比0.5偏大,在50000时又比0.5偏小，偏差幅度越来越小，的确有收敛到0.5的趋势
说得不是很清楚。
好神奇。
再看一篇，终于看懂了，以前看忽略了最关键的一句，“我们把连续的相同数看作一组”。
所以对14楼的解释就是，a(1)=1表示第一组只有一个数，这个数就是1，而第二组的数必然不能等于第一组，所以a(2)=2;
还是你提醒了我
定义应该写成“数列{a}，a(1)=1…”，不然还以为a只是个function呢。
a(1) = 1 就表明第一组数只有一个数，因此下一个数必须要换成 2 ，因此 a(2) = 2
第一个因此知道原因，第二个就不是怎么因此了，也可以a(2)=1啊
数列的定义好像不够完整，应该补充上：用b[n]表示该数列（b[i]=1或者b[i]=2，i=1,2,3,……）第i位的值。然后a[n]表示第n组数的长度，并且a[n]=b[n]。
回20楼
注意关键句，“我们把连续的相同数看作一组”。
如果a(2)=1，那么因为a(1)=a(2),所以它们是同一组数，即同属于第一组数，第一组数就有两个，而a(1)=1定义了第一组数只能有一个。二者矛盾，所以a(2)不能为1
1) The only numbers allowed are 1 and 2
2) Each number tells us how many numbers to append to the sequence
2a) 1 tells us to append one more number
2b) 2 tells us to append two more numbers
3) We can have no more than two of the same number in sequence
3a) This is because if we write 222 that means that somewhere in the sequence it told us to append 3 twos, but the only numbers allowed are 1 and 2
4) Every time we “read” a new number, we alternate between writing 1 and 2
5) A0=1
转载自：http://en.wikipedia.org/wiki/Kolakoski_sequence
感觉还是这个说的详细
感觉你描述得不是很清楚。
是不是第i组的长度等于第i个字符的意思？
终于搞明白了，lz这个描述实在不清楚，22楼更是越说越乱。这个数列是an，第n项表明第n组数的长度所以第一组长度是1，写下1，然后就要把数字换成2，这又表明第二组数有两个数，所以是122，第三组数又两个，12211，第四组数一个，122112…………楼主说的另一种解释应该表述为：把每组数长度依次写下来，就是该数列
25楼说的明白些，23楼提供的很不错。
我用C#写了一个，运行到1亿次
得到的结果如下：最后2位是1和2
总次数：100000000
1出现的次数：50000674
概率：0.50000674
下面是一些数据：3列分别为 总次数 1出现的次数 出现概率
10000 4995 0.4995
100000 49971 0.49971
1000000 499985 0.499985
10000000 5000045 0.5000045
100000000 50000674 0.50000674
另外1和2出现的次数会间歇性的相等，
它们出现次数相等的情况一亿次内共发生了34537次
根据这些数据，我想我可以下结论了。
期待大家的检验，邮箱combeta@live.com。
这么复杂 你解答出来了吗
很好，很强大！！
说得不是很清楚。
看了 猥疯 的评论终于懂了！！！谢了
heheql
看了 猥疯 的评论终于懂了！！！谢了
—————————————————-
你好，能不能删除一下我的评论，以及现在这条。
牛逼啊