2008-02-05 23:30| 
8 Comments | 本文内容遵从
在数学中，比较运算是有传递性的。如果A>B，且B>C，那么一定有A>C。但现实生活中却不一定是这样。三个人两两之间进行比赛，有可能A比B要强，B比C要强，但C反过来赢了A。事实上，这种现象即使在数学中也是存在的。在一些概率事件中，类似的“大小关系”很可能并不满足传递性。
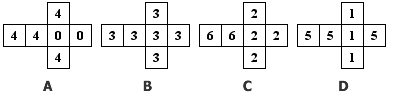
右边有四颗骰子，分别用A、B、C、D来表示。我让你先选择一颗你自己认为最好的骰子，然后我再从剩下的三个骰子中选一个。抛掷各自所选的骰子后，谁掷出的数字大，谁就赢了。那么，你应该选哪颗骰子好呢？
其实，不管你选哪一个骰子，我获胜的概率总是要大一些，因为剩下的三个骰子中总有一个骰子比你的要好。事实上，在这四颗骰子中，A赢B的概率是2/3，B赢C的概率是2/3，C赢D的概率是2/3，D赢A的概率还是2/3，因此不管你选的是哪一个骰子，只要我选择它左边的那一个（如果你选的是最左边的，则我选择最右边的），我总保证有2/3的概率获胜。你认为这样的事情有可能吗？对你来说这样的事情合乎情理吗？
如果你不信的话，我们可以一起来算一算：
A和B比时，只要A扔出4的话A就赢了，这有2/3的概率；
B和C比时，只要C扔出2的话B就赢了，这有2/3的概率；
C和D比时，若C扔出6则C一定能赢，若C扔出2则胜负几率对等，因此C获胜的概率是(1/3) + (2/3)*(1/2) = 2/3；
D和A比时，若A扔出0则D一定能赢，若A扔出4则胜负几率对等，因此D获胜的概率是(1/3) + (2/3)*(1/2) = 2/3。
8 条回复
您也随便说几句吧：
沙发
Matrix67 果然是赖皮的好手……
晕，这是有概率呵
拿这要骗MM的话，万一掷到1/3就囧了……
可以多次重复游戏，这样还是你的赢面大。
而且，得让MM也小小赢几盘，否则她觉得你使诈，就不玩了。。。
实际上确实存在一个最好的色子C。
这个色子如果和它左边的色子B比，获胜的概率（从场次上来说）小，但是掷出的数字的期望比左边的色子大。也就是说，虽然总是输，但是总输的点数不多（不管怎么说按照这个规则输了就是输了）；一旦赢一场，就赢很多点。
（反正这要看游戏规则怎么定，如果是积分制的，那C胜算最大）
回复：嗯，我也是这样认为的
我做这个选择的时候就是单纯的用数学期望考虑的，选的C，呵呵。
m牛（我也跟着大家这么叫哈）这里的确有很多很有意思的东西。开学的时候就要带本本了，到时候给武大的哥们好好宣传宣传，看看咱们的兄弟有多么强！呵呵呵呵呵……
成功引用4个色子向MM证明大于传递不成立,
MM一脸困惑.
为什么会这样