前几天，一篇叫做 用正方形纸片折出等边三角形 的日志引起大家的讨论，折出正七边形和折出角三等分线的方案更是让大家争论不休。提得最多的问题就是，折纸为什么要比尺规作图更强？这是一个好问题。我查了不少资料，了解到不少折纸几何的历史，收获颇大，不赶紧记下来就亏大了。于是有了这篇文章。

    要解答为何折纸如此强大，首先我们得解决一个问题：什么叫折纸。折纸的游戏规则是什么？换句话说，折纸允许哪些基本的操作？大家或许会想到一些折纸几何必须遵守的规则：所有直线都由折痕或者纸张边缘确定，所有点都由直线的交点确定，折痕一律是将纸张折叠压平再展开后得到的，每次折叠都要求对齐某些已有几何元素（不能凭感觉乱折），等等。不过，这些定义都太“空”了，我们需要更加形式化的折纸规则。 1991 年， Humiaki Huzita 指出了折纸过程中的 6 种基本操作（也可以叫做折纸几何的公理）：

   

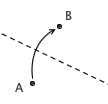
 1. 已知 A 、 B 两点，可以折出一条经过 A 、 B 的折痕

   

 2. 已知 A 、 B 两点，可以把点 A 折到点 B 上去（想象这张纸是透明的，所有几何对象正反两面都能看见，下同）

   

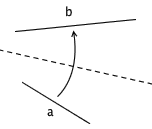
 3. 已知 a 、 b 两条直线，可以把直线 a 折到直线 b 上去

   

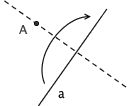
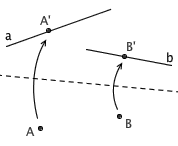
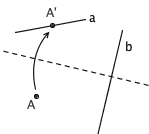
 4. 已知点 A 和直线 a ，可以沿着一条过 A 点的折痕，把 a 折到自身上

   

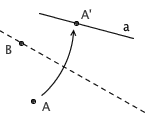
 5. 已知 A 、 B 两点和直线 a ，可以沿着一条过 B 点的折痕，把 A 折到 a 上

   

 6. 已知 A 、 B 两点和 a 、 b 两直线，可以把 A 、 B 分别折到 a 、 b 上

    容易看出，它们实际上对应着不同的几何作图操作。例如，操作 1 实际上相当于连接已知两点，操作 2 实际上相当于作出已知两点的连线的垂直平分线，操作 3 则相当于作出已知线段的夹角的角平分线，操作 4 则相当于过已知点作已知线的垂线。真正强大的则是后面两项操作，它们确定出来的折痕要满足一系列复杂的特征，不是尺规作图一两下能作出来的（有时甚至是作不出来的）。正是这两个操作，让折纸几何有别于尺规作图，折纸这门学问从此处开始变得有趣起来。

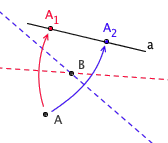
    更有趣的是，操作 5 的解很可能不止一个。在大多数情况下，过一个点有两条能把点 A 折到直线 a 上的折痕。

    

    操作 6 则更猛：把已知两点分别折到对应的已知两线上，最多可以有三个解！

    

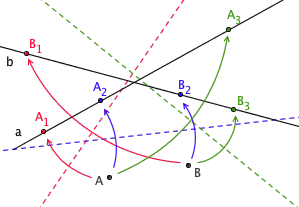
    一组限定条件能同时产生三个解，这让操作 6 变得无比灵活，无比强大。利用一些并不太复杂的解析几何分析，我们能得出操作 6 有三种解的根本原因：满足要求的折痕是一个三次方程的解。也就是说，给出两个已知点和两条对应的已知线后，寻找符合要求的折痕的过程，本质上是在解一个三次方程！

    让我们来回顾一下尺规作图里的五个基本操作：

 1. 过已知两点作直线
 2. 给定圆心和圆周上一点作圆
 3. 寻找直线与直线的交点
 4. 寻找圆与直线的交点
 5. 寻找圆与圆的交点

    这五项操作看上去变化多端，但前三项操作都是唯一解，后两项操作最多也只能产生两个解。从这个角度来看，尺规作图最多只能解决二次问题，加减乘除和不断开方就已经是尺规作图的极限了。能解决三次问题的折纸规则，势必比尺规作图更加强大。

    正因为如此，一些尺规作图无法完成的任务，在折纸几何中却能办到。这就回到了文章开头提到的问题：用折纸法可以实现作正七边形，而这是无法用尺规作图办到的。

    我们有更简单的例子来说明，用折纸法能完成尺规作图办不到的事情。“倍立方体”问题是古希腊三大尺规作图难题之一，它要求把立方体的体积扩大到原来的两倍，本质上是求作 2 的立方根。由于尺规作图最多只能开平方，因而它无法完成“倍立方体”的任务。但是，折纸公理 6 相当于解三次方程，解决“倍立方体”难题似乎是游刃有余。

    有意思的是，用纸片折出 2 的立方根比想象中的更加简单。取一张正方形纸片，将它横着划分成三等份（方法有很多，大家不妨自己想想）。然后，将右边界中下面那个三等分点折到正方形内上面那条三等分线上，同时将纸片的右下角顶点折到正方形的左边界。那么，纸片的左边界就被分成了 ³√2 : 1 两段。

    

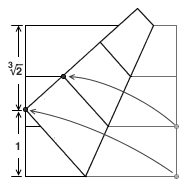
    利用勾股定理和相似三角形建立各线段长度的关系，我们不难证明它的正确性。强烈建议大家自己动笔算一算，来看看三次方程是如何产生的。

    本文写到这里，大家或许以为故事就结束了吧。 10 年以后（也就是 2001 年），事情又有了转折： Koshiro Hatori 发现， Humiaki Huzita 的 6 个折纸公理并不是完整的。 Koshiro Hatori 给出了折纸的第 7 种操作。从形式上看，第 7 公理与已有的公理如出一辙，并不出人意料，很难想象这个公理整整十年里竟然一直没被发现。继续阅读之前，大家不妨先自己想想，这个缺失的操作是什么。这段历史背景无疑让它成为了一个非常有趣的思考题。

 
 
 
    Koshiro Hatori 补充的公理是：

   

 7. 已知点 A 和 a 、 b 两直线，可以沿着一条垂直于 b 的折痕，把 A 折到 a 上。

    后来，这 7 条公理就合称为了 Huzita–Hatori 公理，你可以在 Wikipedia 上读到这个条目。在 2003 年的一篇文章中， Robert J. Lang 对这些公理进行了一番整理和分析，证明了这 7 条公理已经包含折纸几何中的全部操作了。

    Robert J. Lang 注意到了，上述 7 项基本操作其实是由一些更基本的操作要素组合而成的，例如“把已知点折到已知线上”、“折痕经过已知点”等等。说得更贴切一些，这些更加基本的操作要素其实是对折痕的“限制条件”。在平面直角坐标系中，折痕完全由斜率和截距确定，它等价于一个包含两个变量的方程。不同的折叠要素对折痕的限制力是不同的，例如“把已知点折到已知点上”就同时要求 x₁‘ = x₂ 并且 y₁‘ = y₂ ，可以建立出两个等量关系，一下子就把折痕的两个变量都限制住了。而“折痕经过已知点”则只能列出一个方程，只能确定一个变量（形式上通常表示为与另一个变量的关系），把折痕的活动范围限制在一个维度里。

    不难总结出，基本的折叠限制要素共有 5 个：

 (1) 把已知点折到已知点上，确定 2 个变量
 (2) 把已知点折到已知线上，确定 1 个变量
 (3) 把已知线折到已知线上，确定 2 个变量
 (4) 把已知线折到自身上，确定 1 个变量
 (5) 折痕经过已知点，确定 1 个变量

    而折痕本身有 2 个待确定的变量，因此符合要求的折纸操作只有这么几种： (1) ， (2)+(2) ， (3) ， (4)+(4) ， (5)+(5) ， (2)+(4) ， (2)+(5) ， (4)+(5) 。但是，这里面有一种组合需要排除掉： (4)+(4) 。在绝大多数情况下， (4)+(4) 实际上都是不可能实现的。如果给出的两条直线不平行，我们无法折叠纸张使得它们都与自身重合，因为没有同时垂直于它们的直线。

    另外 7 种则正好对应了前面 7 个公理，既无重合，又无遗漏。折纸几何至此便有了一套完整的公理。

    不过，折纸的学问远远没有到此结束。如果允许单次操作同时包含多处折叠，折纸公理将会更复杂，更强大。折纸的极限究竟在哪里，这无疑是一个非常激动人心的话题。