除了正多面体，骰子还可以做成哪些形状？

   

    上图的拍摄者一定是个桌游达人，五种正多面体骰子的全家福竟然都能被他搞出来。我们自然会想到一个有趣的问题：还有别的形状的骰子吗？或者更“数学”一些的说法，在凸多面体的每个面上都标一个数字，能用来当骰子的就只有这五种吗？看上去似乎是这样：只有正多面体才能保证这颗骰子是“公平”的。呃⋯⋯是吗？


    事实上，对于骰子来说， 正多面体不是必要的。至少不需要那么“正”——只需要满足多面体每个面的地位都相同就可以了。例如，取两个全等的正 n 棱锥，底面和底面互相粘在一起，就能得到一个有 2n 个面的多面体。

   

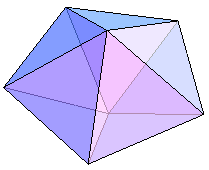
    这个多面体不是正多面体，不同顶点所处的位置是有区别的，不同的棱也有本质上的区别。不过，这个多面体的每个面的情况都是一样的，这就足以让它成为一颗公正的骰子了。

    有没有同样满足要求，但却没这么“平凡”的多面体呢？还真有不少。下图是把四个相同的三棱锥分别粘在一个正四面体的各面得到的十二面体。

   

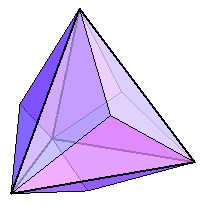
    满足要求的最简单的多面体则是这样一个四面体，它由一个长方体 6 个面上的对角线组成。

   

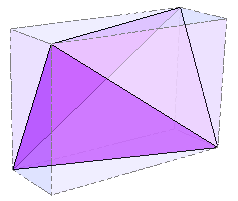
    这个四面体看上去似乎很不规则，但仔细看看便能看出，它的每个面恰好都是一个由三种不同长度的棱组成的三角形，并且这三条棱各自的另一侧正好分别对应着另外的三个面。因此，这是一个满足要求的多面体。

    类似的多面体还有很多，这里有一个图鉴，有兴趣的读者不妨前去围观。

 
    其实，可以用来当骰子的多面体要求还可以更松一些。如果在一个多面体中，所有面可以分成 n 组，每一组的形状和地位都完全相等，那么我们也可以把它做成一颗有 n 个“广义面”的骰子。下图便是一个简单的例子。

   

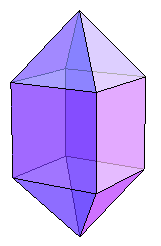
    我们可以把上面这个多面体的 12 个面分成四组，每组各含一个正方形和两个三角形。由于不同的组之间没有本质区别，因此把第 i 组里的三个面都标上数字 i ，或者干脆大手笔地在整组面上标数字，一颗符合要求的骰子就诞生了。套用这种方法，我们可以生成面的组数任意多并且每一组包含面数也任意多的骰子。

    非平凡的此类多面体也是有的。下图便是一个由 4 个正方形和 4 个正三角形拼成的八面体。

   

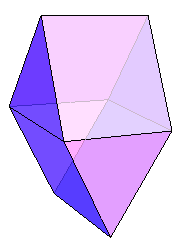
    这个图形大致可以看作是有四个“侧面”。如果把这些“侧面”分别标作 1 、 2 、 3 、 4 ，也可以成为一个符合要求的骰子。

    如果你对这个话题感兴趣，欢迎继续阅读：
    http://loki3.com/poly/fair-dice.html
    http://www.maa.org/editorial/mathgames/mathgames_05_16_05.html

    如果你对各种诡异形状的骰子感兴趣，你一定会喜欢这个：
    http://www.dicecollector.com/DICEINFO_WHAT_SHAPES_DO_DICE_HAVE.html

33 条评论

发表评论

6  ×    =  42