考虑复数域上的迭代公式 zn+1 = zn^2 + (- 0.123 + 0.745 i) 。取不同的初始值 z0 ,迭代后 zi 的发散速度是不一样的。对于复平面上的每个点,以它为初始值的数列发散速度越快,就染越深的颜色表示;如果以它为初始值数列发散缓慢甚至收敛,则用相对较浅的颜色来表示。那么,整个图形将会是什么样子呢?本人纯手工打造 Mathematica 代码两行,为大家送上这幅神奇的图形:
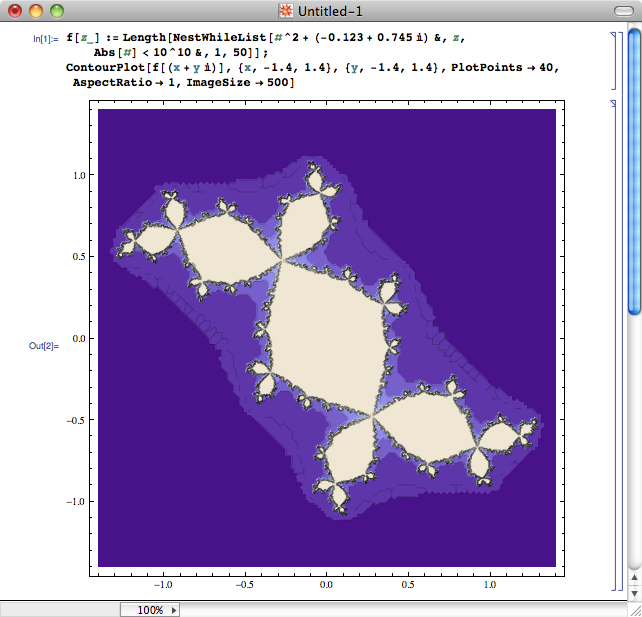
难以置信,简单的公式竟然生成了如此复杂的分形图形,看上去仿佛是大大小小的兔子竖着耳朵跳出来给大家拜年一样。这个图形叫做 Douady 兔子,是由法国数学家 Adrien Douady 发现的。它是一种 Julia 集。