出租车几何学：一个全新的几何世界

    从北大打车到四惠，我一定会选择走四环。虽然从北京城中间直穿过去看上去很诱人，但考虑到北京道路几乎总是正南正北的方向，不会真有人认为这样能抄近路吧。在城市中，我们估算两点之间的距离时，往往不会直接去测量两点之间的直线距离，而会去考虑它们相距多少个街区。在理想模型中，假设每条道路都是水平或者竖直的，那么只要你朝着目标走（不故意绕远路），不管你怎样走，花费的路程都是一样的。今天，我看到了一个非常有意思的名词——出租车几何学 (taxicab geometry) ，其名称就来源于这样的想法。

  

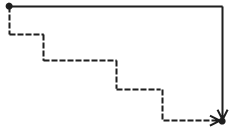
    在出租车几何学中，点还是形如 (x, y) 的有序实数对，直线还是满足 a x + b y + c = 0 的所有 (x, y) 组成的图形，角度大小的定义也和原来一样。只是，(x1, y1) 和 (x2, y2) 的距离重新定义为了 |x1 – x2| + |y1 – y2| ，即两点的横坐标之差加上纵坐标之差。

    这是一个对“距离”的合理定义，因为它满足

  • 非负性：两点距离总是大于等于 0
  • 对称性： A 到 B 的距离等于 B 到 A 的距离
  • 零距离： A 到 B 的距离为 0 当且仅当 A = B
  • 三角形不等式：对于任意三点 A 、 B 、 C ，不等式 AB + BC ≥ AC 总成立

    也就是说出租车几何学是建立在一个合理的度量空间上的。这是一个全新的几何世界。


    在这个世界里，很多经典几何定理仍然成立。比方说，三角形的内角和还是 180 度。因为，这是一个关于角度的定理，与距离的度量方式无关；既然角度的度量方式不变，三角形的内角和也仍然不会变。

  

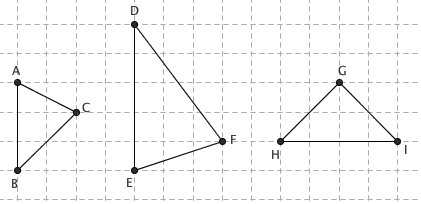
    不过，一旦涉及到三角形的边长，很多基本命题就不再成立了。等边对等角是首先被否定掉的定理，底角不相等的等腰三角形满地都是。例如上图中的三角形 ABC ，虽然 AB = AC ，但三角形的两个底角显然不等。类似地，等角对等边也不成立了，例如右图中虽然角 E 和角 F 相等，但 DE = 5 ， DF = 7 。 更不可思议的是，在出租车几何中，甚至能画出等边直角三角形来！

  

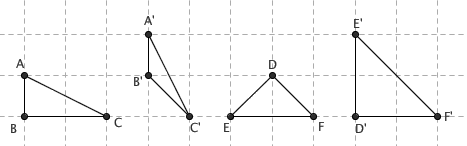
    在这个几何世界中，边边边不能用来判断三角形全等了。我们可以画出两个三角形 ABC 和 A’B’C’ ，它们的对应边都相等，但这两个三角形并不能重合在一起。边角边也不能作为全等三角形的判定依据了——三角形 DEF 和 D’E’F’ 都是直角边均为 2 的直角三角形，不过它们明显不全等。

 
    真正有趣的不是出租车几何学世界中的三角形，而是这个世界中的圆。我们仍然定义圆是所有到定点距离为定值的点组成的图形。那么在这个几何世界里，圆是什么样的？下图给出了这个几何世界中一个半径为 2 的圆，圆周上的所有点到 O 的距离均为 2 ：

  

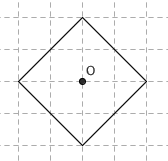
    惊奇的不止这一点。圆的方程似乎更简单了，以原点为圆心的单位圆对应的方程是 |x| + |y| = 1 。更神奇的是，这个几何世界的圆周率值也不一样了，它精确地等于 4 ！

 
    重新定义距离后，很多图形会变得更加复杂。定义两点间的垂直平分线为到两点距离相等的点组成的图形。在这个几何世界里，垂直平分线是什么样的？在一般情况下，垂直平分线并不是“垂直”平分线，而是一条折线段。

  

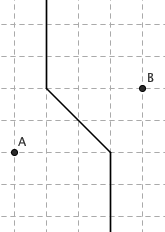
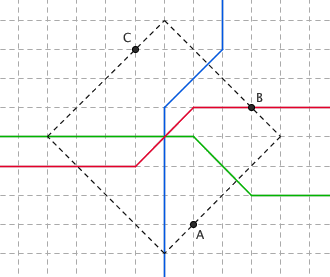
    但尽管垂直平分线如此奇怪，不过（一般情况下）三角形三边的垂直平分线仍然交于一点。这是因为，“三角形三边的垂直平分线交于一点”的证明过程只与垂直平分线的定义有关，而与垂直平分线的具体形式是无关的。即使证明过程用到了距离的定义，用到的也是新旧两种定义共有的一些基本性质。更有趣的是，这个点也是名副其实的“外心”，以它为中心可以作出这个三角形的外接圆来！也就是说，在出租车几何里，一般位置上的三个点也唯一地确定了一个圆。

  

    不过，也有一些特殊的情况，三点不能确定一个圆。比方说，同时过 (0, 1) 、 (0, -1) 、 (1, 0) 的圆就有无穷多个。这是因为，(0, 1) 和 (1, 0) 的垂直平分线，以及(0, -1) 和 (1, 0) 的垂直平分线都不是“线”，有整块区域的点都满足到两端点的距离相等。因此这几条“垂直平分线”的交集不止一个点。

 
    还有哪些欧氏几何的经典结论在出租车几何学中同样成立？出租车几何学中有什么漂亮而独特的结论？如何定义一些更加复杂的几何对象？它们在出租车几何学中又是什么样？大家不妨继续往下思考一下。

50 条评论

发表评论




Enter Captcha Here :